Kryssprodukt - areal og volum

Areal

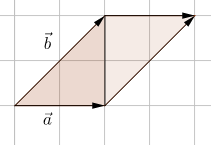
Arealet av et parallellogramm er bestemt av vektorene $\vec{a}$ og $\vec{b}$ er gitt ved $|\vec{a}\times \vec{b}|$. Arealet av en trekant utspent av to vektorer, er halvparten av arealet til parallellogramet.

Da får vi at arealet til trekanten er $$\frac{1}{2}|\vec{a}\times \vec{b}|.$$

Eksempel 1

Vi er gitt punktene $A=(1,1,0)$, $B=(3,4,0)$ og $C=(4,2,0)$. Som tidligere tenker vi at punktene ligger i $xy$-planet i tredimensjonalt rom. Vi ønsker å finne arealet av trekanten $\Delta ABC$. Vi finner vektorene $\overrightarrow{AB}=[2,3,0]$ og $\overrightarrow{AC}=[1,-2,0]$. Vi regner ut kryssproduktet: $$\overrightarrow{AB}\times \overrightarrow{AC}=\mid \begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ 2& 3& 0\\ 1& -2& 0\end{array}\mid =\vec{k}\mid \begin{array}{cc}2& 3\\ 1& -2\end{array}\mid =[0,0,-7].$$ Lengden til denne vektoren er $7$. Dermed er arealet til trekanten $\frac{7}{2}$.

Volum

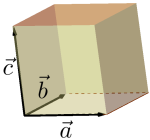
Gitt tre vektorer $\vec{a},\vec{b}$ og $\vec{c}$ i planet kommer disse til å spenne et parallellepiped, en figur med seks parallellogrammer som sideflater.

Volumet er gitt som produktet av arealet av grunnflaten og høyden. Arealet av grunnflaten $G$ er $$G=|\vec{a}\times \vec{b}|.$$ Siden vektoren $\vec{a}\times \vec{b}$ står normalt på grunnflaten, er høyden gitt ved $\left|\vec{c}\right|\cdot \cos \theta$ hvor $\theta$ er vinkelen mellom $\vec{c}$ og $\vec{a}\times \vec{b}$. Vi konkluderer med at volumet $V$ er gitt ved $$V=|\vec{a}\times \vec{b}|\cdot \left|\vec{c}\right|\cdot \cos \theta .$$ Vi kjenner igjen denne formelen fra vinkelen mellom to vektorer, dette er simpelthen $$V=(\vec{a}\times \vec{b})\cdot \vec{c}.$$ Her har vi ikke tatt hensyn til fortegn slik at vi bruker absoluttverdien av tallet dersom negativt.

Eksempel 2

Vi regner ut volumet av parallellepidedet som spennes ut av $\vec{a}=[4,1,1],\vec{b}=[1,4,2]$ og $\vec{c}=[2,2,4]$. Vi må først regne ut $\vec{a}\times \vec{b}$: $$\vec{a}\times \vec{b}=\mid \begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ 4& 1& 1\\ 1& 4& 2\end{array}\mid =-2\vec{i}-7\vec{j}+15\vec{k}=[-2,-7,15].$$ Nå kan vi regne ut volumet: $$(\vec{a}\times \vec{b})\cdot \vec{c}=[-2,-7,15]\cdot [2,2,4]=-4-14+60=42.$$

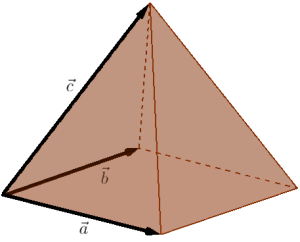
Om vi vil regne ut volumet av en pyramide hvor grunnflaten er et parallellogram kan vi også gjøre dette som vanlig.

Vi vet at volumet av pyramiden er $$\frac{1}{3}Gh$$ hvor $G$ er arealet av grunnflaten og $h$ er høyden. Men vi har nettopp regnet ut at $Gh=(\vec{a}\times \vec{b})\cdot \vec{c}$. Dermed er volumet av pyramiden $$V=\frac{1}{3}(\vec{a}\times \vec{b})\cdot \vec{c}.$$

Eksempel 3

En pyramide er spent ut av vektorene $\vec{a}=[4,1,-1]$, $\vec{b}=[3,2,1]$ og $\vec{c}=[1,3,0]$. Vi regner først ut $\vec{a}\times \vec{b}$: $$\vec{a}\times \vec{b}=\mid \begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ 4& 1& -1\\ 3& 2& 1\end{array}\mid =3\vec{i}-7\vec{j}+5\vec{k}=[3,-7,5].$$ Vi regner ut volumet:

$V=\frac{1}{3}(\vec{a}\times \vec{b})\cdot \vec{c}=\frac{1}{3}\left(\right[3,-7,5]\cdot [1,3,0\left]\right)=\frac{1}{3}(3-21+0)$ 

$V=\frac{1}{3}\cdot (-18)=-6.$

Siden tallet er negativt må vi ta absoluttverdi. Dermed er volumet $6$.

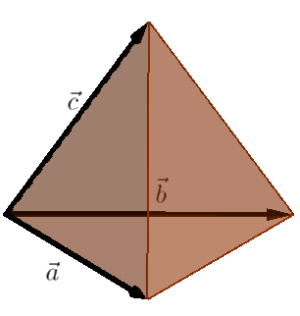
Som et siste eksempel kan vi bruke de samme teknikkene til å finne volumet av et tetraeder, hvor grunnflaten er en trekant.

I dette tilfellet vet vi at arealet av grunnflaten er $\frac{1}{2}|\vec{a}\times \vec{b}|$. Dermed er volumet likt

$$V=\frac{1}{3}\left(\frac{1}{2}\left(\overrightarrow{a}\times \overrightarrow{b}\right)\cdot \overrightarrow{c}\right)=\frac{1}{6}\left(\overrightarrow{a}\times \overrightarrow{b}\right)\cdot \overrightarrow{c}.$$

Eksempel 4