Subtraksjon av vektorer

Å subtrahere en vektor kan tenkes som å forflytte seg like langt som den, men i motsatt retning.

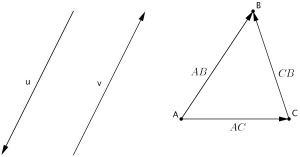
Hvis vi først legger til en vektor og så trekker fra den samme vektoren, ønsker vi å komme tilbake til utgangspunktet. Den motsatte av vektoren fra $A$ til $B$ er vektoren fra $B$ til $A$ .

Definisjon

$\vec{A B} og \vec{B A}$ er motsatte vektorer. Vi skriver $\vec{- A B} = \vec{B A}$ .

$\vec{u} og \vec{- u}$ er motsatte vektorer. De er like lange, men har motstatt retning.

Dette betyr at å subtrahere en vektor er det samme som å addere den motsatte vektoren.

Vektorene $\vec{u}$ og $\vec{v}$ er motsatte vektorer; de har samme lengde, men er motsatt rettet. På bildet over til høyre ser vi $\vec{A C} = \vec{A B} - \vec{C B} = \vec{A B} + \vec{B C}$ .

SUBTRAKSJON AV VEKTORER PÅ KOORDINATFORM

La $\vec{u} = [x_{1}, y_{1}]$ og $\vec{v} = [x_{2}, y_{2}]$ være to vektorer. Vi subtraherer vektorer koordinatvis, det vil si

$\vec{u} - \vec{v} = [x_{1}, y_{1}] - [x_{2}, y_{2}] = [x_{1} - x_{2}, y_{1} - y_{2}] .$

Eksempel 1

$[5, 11] - [1, 9] = [5 - 1, 11 - 9] = [4, 2]$

Eksempel 2

$[6, 0, - 2] - [1, 1, 1] = [6 - 1, 0 - 1, - 2 - 1] = [5, - 1, - 3]$

Del på Facebook

Del på Facebook

Subtraksjon av vektorer

Eksempel 1

Eksempel 2

Lynkurs 11.-13.trinn

Vektorer

Består av: