Parametriserte kurver

Parameterfremstillinger av rette linjer er alltid på formen $$\{\begin{array}{c}x=x_0+at\\ y=y_0+bt.\end{array}$$ Dette betyr at linjen går gjennom punktet $(x_0,y_0)$ og er parallell med vektoren $[a,b]$. Nå skal vi gi oss selv litt mer frihet, og la $x$ og $y$ være vilkårlige funksjoner avhengig av en parameter $t$: $$\{\begin{array}{c}x=x\left(t\right)\\ y=y\left(t\right).\end{array}$$

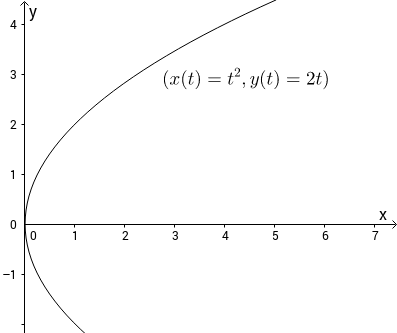
Eksempel 1

Parameterfremstillingen $$\{\begin{array}{c}x=t^2\\ y=2t\end{array}$$ gir oss følgende bilde:

For alle verdier av $t$ kommer parameterfremstillingen til å gi oss et punkt $\left(x\right(t),y(t\left)\right)$ i planet.

Parametriserte kurver kan vi også se å på som vektorfunksjoner.

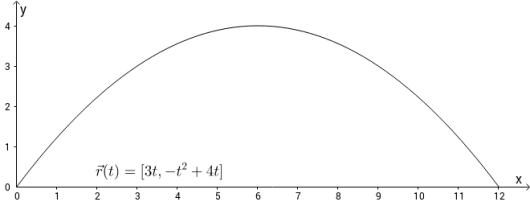
Eksempel 2

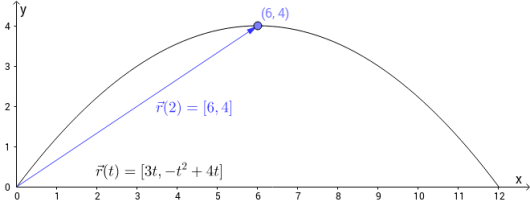
Parameterfremstillingen $$\{\begin{array}{c}x=t^2\\ y=2t\end{array}$$ har vektorfunksjonen $\vec{r}\left(t\right)=[t^2,2t]$. Velger vi $t=1$, får vi punktet $(1,2)$ i planet. Retningsvektoren er $\vec{r}\left(1\right)=[1,2]$ og vi illustrerer det på følgende måte:

For rette linjer får vi vektorfunksjonen $\vec{r}\left(t\right)=[x_0+at,y_0+bt]$. Husk at denne linjen alltid er parallell med vekoten $[a,b]$. Det er nøyaktig denne vektoren vi får når vi deriverer vektorfunksjonen i hvert koordinat, $\vec{r}\prime \left(t\right)=[a,b]$. Denne vektoren kalles fartsvektoren til linjen. Dette er noe vi kan gjøre for alle parametetriserte kurver.

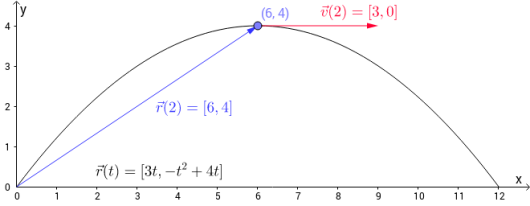
Eksempel 3

Vi ser igjen på parameterfremstillingen med vektorfunksjon $\vec{r}\left(t\right)=[t^2,2t]$. Vi deriverer i hvert koordinat og får $\vec{v}\left(t\right)=[2t,2]$. Ved $t=1$, får vi fartsvektoren $\vec{v}\left(1\right)=[2,2]$. Farten til kurven ved $t=1$ gitt ved $$\left|\vec{v}\right(1\left)\right|=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}.$$ 

Merk at fartsvektoren (i rødt) tangerer kurven.

Eksempel 4

Stian kaster en ball i fysikktimen. Etter $t$ sekunder er posisjonen til ballen gitt ved $$\{\begin{array}{c}x=3t\\ y=-t^2+4t\end{array}$$ for $0\le t\le 4$, hvor $x$ og $y$ er lengde og høyde i meter. Vi ønsker å finne hvor høyt ballen er etter $2$ sekunder, og farten til ballen ved denne tiden. Vektorfunksjonen til kurven er $\vec{r}\left(t\right)=[3t,-t^2+4t]$: 

Da er $$\vec{r}\left(2\right)=[6,4].$$ 

Høyden, $y$-koordinatet, er $4$ meter. For å finne farten deriverer vi funksjonen i hvert koordinat og får at $$\vec{v}\left(t\right)=[3,-2t+4].$$ Når $t=2$, er fartsvektoren $\vec{v}\left(2\right)=[3,0]$. Dermed er farten $$\left|\vec{v}\right(2\left)\right|=\sqrt{3^2+0^2}=3.$$