Parameterframstilling av en rett linje

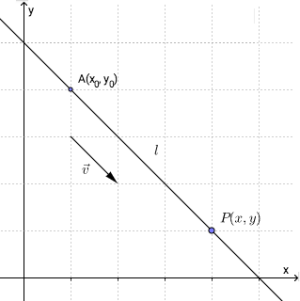
Når vi skal finne en parameterframstilling for en rett linje, kan vi ta utgangspunkt i en

og et fast punkt på linjen. Vi bruker en ekstra variabel, som oftest $t$ som kalles parameter.

Vi kaller $\overrightarrow{v}$ en retningsvektor for linja. Legg også merke til at det finnes mange parameterframstillinger for en og samme linje. Det er avhengig av hvilken punkt og retningsvektor vi velger.

Eksempel 1.

La oss sette opp en parameterframstilling for en normal $n$ på $y$ - aksen i punktet $\left(0,3\right)$. Likningen for

 $n$ er $y=3$, fordi alle punktene på $n$ har $3$ som andrekoordinat, mens førstekoordinat kan være hva som helst. Normalen $n$ har parameterframstillingen som følger

$n:\left\{\begin{array}{c}x=t\\ y=3\end{array}\right.$

Legg merke til at retningsvektoren er $\overrightarrow{v}=\left[1,0\right]$ (siden det er normalen på $y$ - aksen). Vi kunne derimot like gjerne ha valgt retningsvektoren $\overrightarrow{v}=\left[6,0\right]$ og fått følgende parameterframstilling

$n:\left\{\begin{array}{c}x=6t\\ y=3\end{array}\right.$

Sett inn for eksempel $3\mathrm{for}t$ i den første parameterframstilligen. Vi får punktet $\left(3,3\right)$. Hvis vi velger $\frac{3}{6}$ for $t$ i den andre parameterframstillingen, får vi også punktet $\left(3,3\right)$.

 

 

 

Eksempel 2.

Den rette linjen $j$ går gjennom punktene $A\left(1,1,0\right)\mathrm{og}B\left(0,1,2\right)$.

For å finne parameterframstillingen til linjen, regner vi først ut vektoren $\overrightarrow{AB}$ og bruker denne som retningsvektor.

$\overrightarrow{AB}=\left[1-0,1-1,0-2\right]=\left[1,0,-2\right]$

Parameterframstillingen for $j$ er

$j:\left\{\begin{array}{c}x=1-t\\ y=1\\ z=-2t\end{array}\right.$$z=8$

 

For å finne ut om et punkt ligger på linjen, undersøker om det finnes en verdi av $t$ ved å bruke koordinatene i punktet på venstresiden av likhetene i parameterframstilligen av linjen. La oss se om punktet $\left(5,1,-9\right)$ ligger på linjen. Da lar vi $x=5$. Da er $5=1-t\mathrm{og}t=-4$. Setter vi $-4$ inn for $t$ i $z=-2t$, får vi at $z=8$. Men i punktet er tredjekoordinaten lik $-9$.

Det finnes ingen verdi av $t$ og derfor er heller ikke punktet på linjen.

 

For å finne et skjæringspunkt mellom $xy$-planet og linjen, bruker vi at i $xy$-planet er $z$-verdien lik null. For at $z$-verdien skal være lik null, må $t$ være lik null. Dette gir oss $x=1\mathrm{og}\left(1,1,0\right)$ er skjæringspunktet mellom $xy$-planet og linjen $j$.