Skalarmultiplikasjon

Multiplikasjon av tall kan tolkes som gjentatt addisjon. For eksempel kan $3 \cdot 4$ tolkes som $4 + 4 + 4$ . Vi kan tenke på samme måte med vektorer.

Å forflytte seg langs vektoren $\vec{u}$ tre ganger etter hverandre er det samme som å forflytte seg langs en vektor som har samme retning som $\vec{u}$ , og som er tre ganger så lang: $\vec{u} + \vec{u} + \vec{u} = 3 \vec{u}$ .

Vi kan si at vi skalerer vektoren med en faktor (et tall) $k .$ Tallet $k$ kalles for en skalar, og operasjonen kalles skalarmultiplikasjon.

Vi har lært at vi kan multiplisere både hele tall, negative tall, brøker og irrasjonale tall. På samme måte kan skalarmultiplikasjon gjelde alle reelle skalarer $k$ .

Eksempel 1

$- \frac{2}{3} \vec{u}$ er en vektor som går i motsatt retning av $\vec{u}$ og som er $\frac{2}{3}$ så lang som $\vec{u}$ .

Eksempel 2

$π \vec{u}$ er vektoren $\vec{u}$ skalert med faktoren $π .$

Eksempel 3

Multipliserer vi vektoren $\vec{A B}$ med skalaren $- 1$ , får vi en vektor som er like lang som $\vec{A B}$ , men har motsatt retning.

SKALARMULTIPLIKASJON MED VEKTORER PÅ KOORDINATFORM

Når vi multipliserer en vektor med et (reelt) tall (ofte kalt en skalar) $s$ , multipliserer vi inn $s$ i hver av koordinatene. La $\vec{v} = [x, y]$ . Da er

$s \vec{v} = s [x, y] = [s x, s y]$

Hva skjer geometrisk med vektoren $\vec{v} = [x, y]$ når vi mulitpliserer den med ulike tall $s$ ? Jo,

for $s = 1$ forandres ikke vektoren.
for $s = - 1$ får vi vektoren $- \vec{v} = [- x, - y]$ , dvs. vi får vektoren med motsatt retning (retningen snus $1 80^{\circ}$ ), men lengden beholdes.

for $| s | > 1$ forlenges vektoren med en faktor $s$ . Hvis $s$ er positiv, beholder vektoren retningen. Hvis $s$ er negativ, er retningen motsatt.
for $s = 0$ får vi vektoren $[0, 0]$ , dvs. punktet origo. Denne vektoren kalles også nullvektoren. Kjært barn har mange navn.
for $0 < | s | < 1$ forkortes vektoren med en faktor $s$ . Hvis $s$ er positiv, beholder vektoren retningen. Hvis $s$ er negativ, er retningen motsatt.

Eksempel 4

$- 1 [3, 4] = [(- 1) \cdot 3, (- 1) \cdot 4] = [- 3, - 4]$

Eksempel 5

$\sqrt{2} [0, 5, \sqrt{2}] = [\sqrt{2} \cdot 0, \sqrt{2} \cdot 5, \sqrt{2} \cdot \sqrt{2}] = [0, 5 \sqrt{2}, 2]$

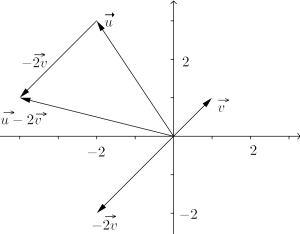
Eksempel 6

La $\vec{u} = [- 2, 3] og \vec{v} = [1, 1]$ . Vi regner ut $\vec{u} - 2 \vec{v}$ :

$[- 2, 3] - 2 [1, 1] = [- 2, 3] + [- 2, - 2] = [- 4, 1] .$

Geometrisk får vi:

Skalarmultiplikasjon bruker vi blant annet for å sjekke om to vektorer er parallelle. For mer om parallelle vektorer, se i høyrespalten.