Omskriving til standardform

 

Eksempel 2

Finn alle løsninger av likningen $-\sin \left(x\right)+\sqrt{3}\cos \left(x\right)=-\sqrt{3}$.

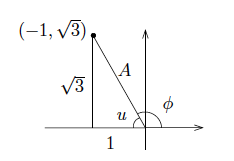
Vi begynner med å skrive venstresiden på standardform. På figuren har vi markert punktet $\left(a,b\right)=\left(-1,\sqrt{3}\right)$. Vi ser at $A=\sqrt{3+1}=2$, og at den inntegnede trekanten er en ${30}^{\circ }-60^{\circ }-{90}^{\circ }-$trekant som du kan lese mer om i artikkelen Trekant. Spesielt er $u={60}^{\circ },$ og derfor er $\phi ={180}^{\circ }-u={120}^{\circ }=\frac{2\pi }{3}.$ Vi kan dermed skrive

$$-\sin \left(x\right)+\sqrt{3}\cos \left(x\right)=2\sin \left(x+\frac{2\pi }{3}\right)$$ Vår opprinnelige likning blir dermed redusert til $2\sin \left(x+\frac{2\pi }{3}\right)=-\sqrt{3}$, eller $\sin \left(u\right)=\frac{1}{2}\sqrt{3}$ , der $u=x+\frac{2\pi }{3}$.

, og et raskt blikk på enhetssirkelen, viser at $\sin \left(-\frac{\pi }{3}\right)=-\frac{1}{2}\sqrt{3}$ . Det betyr at $u=-\frac{\pi }{3}$ er en løsning i likningen over. Da vet vi at alle løsningene er på formen 

$$\left\{\begin{array}{cc}u=& -\frac{\pi }{3}+k\cdot 2\pi \\ u=& \pi -\left(-\frac{\pi }{3}\right)+k\cdot 2\pi \end{array}\right.$$

der $k\in \mathrm{\mathbb{Z}}$.

Til slutt må vi sette tilbake $u=x+\frac{2\pi }{3}$ og løse med hensyn på $x$:

$$\left\{\begin{array}{ccc}x+\frac{2\pi }{3}=& -\frac{\pi }{3}+k\cdot 2\pi & \Rightarrow x=-\pi +k\cdot 2\pi \\ x+\frac{2\pi }{3}=& \pi -\left(-\frac{\pi }{3}\right)+k\cdot 2\pi & \Rightarrow x=\frac{2\pi }{3}+k\cdot 2\pi \end{array}\right.$$

Når $k$ varierer i $\mathrm{\mathbb{Z}}$, gir dette alle løsningene til den opprinnelige likningen.

Selv om de enkelte stegene i løsningen over ikke er vanskelige, er det utfordrende for mange å holde helt til mål i slike oppgaver uten å gjøre slurvefeil. Da er det viktig med oversiktlig føring.