Periodiske funksjoner

Hvordan oppfører trigonometriske funksjonene seg? Funksjonene $\sin x$ og $\cos x$ har en veldig viktig egenskap: de er periodiske.

Vi ser at $\sin x$ og $\cos x$ har denne egenskapen med $a=2\pi$. Når vi jobber med trigonometriske funksjoner kan vi gjøre en hel del funksjonsdrøfting uten å bruke derivasjon, fordi vi allerede vet hvordan topp og bunnpunktene oppfører seg.

Eksempel 1

Vi drøfter funksjonen $f\left(x\right)=4\sin x+2$. For å finne nullpunktene må vi løse likningen $$4\sin x+2=0.$$ Dette kan vi skrive om til $$\sin x=-\frac{1}{2}$$ som gir løsningen $x=-\frac{\pi }{6}$. Vi velger vinkelen i første omløp og bruker løsningen $x=\frac{11\pi }{6}$. Symmetrien om $y$-aksen gir i tillegg $x=\frac{7\pi }{6}$ som en løsning. Den generelle løsningen er $$x=\frac{7\pi }{6}+2\pi n\text{og}x=\frac{11\pi }{6}+2\pi n.$$

Dette er alle nullpunktene til funksjonen. Topp og bunnpunkter kommer når $\sin x$ tar sin største og minste verdi. Vi vet at $\sin x=1$ når $x=\frac{\pi }{2}+2\pi n$, og $\sin x=-1$ når $x=\frac{3\pi }{2}+2\pi n$. I disse tilfellene har funksjonen verdiene $6$ og $-2$.

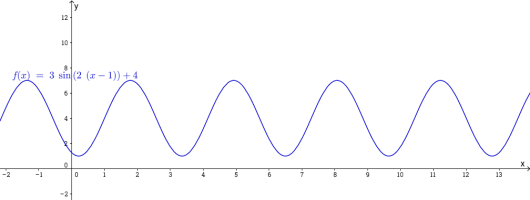
Vi gir nå noen grunnleggende definisjoner ved hjelp av et eksempel. Under har vi tegnet funksjonen til $$f\left(x\right)=3\sin \left(2\right(x-1\left)\right)+4.$$ 

Funksjonen vil svinge rundt likevekstlinjen $y=4$. Den største verdien til funksjonen er $3\cdot 1+4=7$, mens den minste verdien er $3\cdot (-1)+4=1$. Avstanden fra topp- og bunnpunktene til likevektslinjen $y=4$ er lik $3$. Denne avstanden kaller vi amplituden.

Om vi har lyst til å finne perioden til funksjonen $f\left(x\right)$, må vi bruke at funksjonen sinus er periodisk med periode $2\pi$. Vi vet at $$3\sin \left(2\right(x-1)+2\pi )+4=3\sin \left(2\right(x+\pi -1\left)\right)+4=3\sin \left(2\right(x-1\left)\right)+4.$$ Merk at på venstresiden står det $f(x+\pi )$, mens på høyresiden står det $f\left(x\right)$. Dermed har $f$ periode $\pi$, eller $\frac{2\pi }{2}$. Det siste er uttrykket $(x-1)$. Punktet $(1,4)$ er et skjæringspunkt med grafen og likevektslinjen. Merk at $$f\left(1\right)=3\sin 0+4=4.$$

Eksempel 2

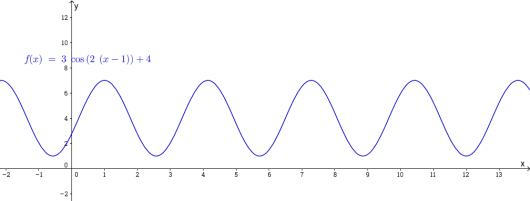
La oss se på funksjonen $\cos$. Om jeg tegner funksjonen $$f\left(x\right)=3\cos \left(2\right(x-1\left)\right)+4$$ får vi følgende bilde:

Vi ser at likevektslinjen $y=4$ er den samme som med sinusfunksjonen. Det samme gjelder amplituden $3$ og perioden $\pi$. Uttrykket $(x-1)$ representerer nå noe annet: nå er $$f\left(1\right)=3\cos 0+4=7.$$ Dette ligger ikke på likevektslinjen $y=4$, men er et toppunkt for funksjonen.

$f\left(x\right)=a\cos \left(k\right(x-c\left)\right)+d$

Eksempel 3

En idrettsutøver lager en treningsplan for et helt år. Hun deler inn årets $52$ uker inn i fire perioder på $13$ uker hver. Alle periodene skal være like. Hun vil ha et snitt på omtrent ti timer trening hver uke, og vil trene maks $17$ timer på en uke og minst $3$ timer. Grunnet konkurranser er det viktig at hun trener $17$ timer i femte uke. Vi blir bedt om å lage en funksjon som kan modellere hvor mye hun skal trene hver uke.

Siden hun har delt inn året i perioder på $13$ uker, og vi vil at periodene skal være like, må funksjonen vår være periodisk med periode $13$. Da passer det fint å bruke et cosinusuttrykk: $$f\left(x\right)=a\cos \left(k\right(x-c\left)\right)+d.$$ Vi vet at perioden til funksjonen er $\frac{2\pi }{k}$. Vi vil at $\frac{2\pi }{k}=13$, dermed må $k=\frac{2\pi }{13}$. Siden snittet skal være omtrent ti timer per uke, velger vi $y=10$ som likevektslinjen. Da er $d=10$. Siden det skal trenes maks $17$ timer og minst $3$ timer, kan vi velge amplituden $a=7$. Siden hun vil trene $17$ timer i den femte uken, sørger vi for at vi får et toppunkt når $x=5$. Det kan vi gjøre ved å velge $c=5$. Da ender vi opp med funksjonen $$f\left(x\right)=7\cos \left(\frac{2\pi }{13}\right(x-5\left)\right)+10.$$