Sinus, cosinus og tangens
I denne seksjonen definerer vi de tre grunnleggende trigonometriske funksjonene: sinus, cosinus og tangens.
De tre
Trigonometriske funksjoner
Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus
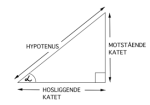
Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
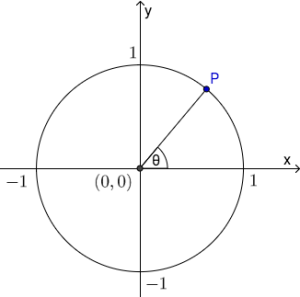
Alle tall definerer en vinkel. Gitt et tall kan vi trekke linjen fra origo med vinkel med hensyn til den positive -aksen. Denne linjen vil treffe et punkt på enhetssirkelen:
Vi kan da definere
Sinus
En trigonometrisk funksjon.
Sinus til en spiss vinkel i en rettvinklet trekant er forholdet mellom lengden til motstående katet og hypotenus.
Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.
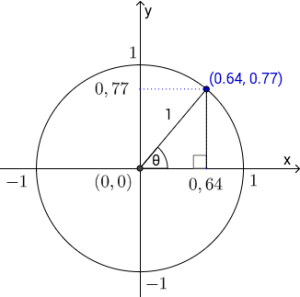
Hypotenusen til denne trekanten har lengde . Merk at lengden til hosliggende og motstående katet er respektivt - og -koordinatene til punktet . Om vi nå definerer cosinus til å være lengden av hosliggende katet og sinus til å være lengden til motstående katet ser vi at dette samsvarer med definisjonen ovenfor. Merk at det følger fra definisjonen og Pytagoras læresetning at
for alle .
Merk at om vi velger en annen radius og konstruerer trekanten på samme måte, får vi en trekant som er formlik med den originale trekanten, da vi kun har forandret lengden på sidene, ikke vinklene. Da kan vi for enhver trekant konstruert på denne måten definere og Disse to funksjonene har definisjonsmengde lik og verdimengde .
Eksempel 1
Vi er gitt en rettvinklet trekant hvor lengden av hypotenusen er centimeter hvor en av vinkelene er og lengden på motstående katet er centimeter. Vi ønsker å finne lengden til hypotenusen. Per definisjon har vi Vi har at , og dermed at centimeter.
Eksempel 2
Vi er gitt en rettvinklet trekant hvor en av vinklene er , lengden på hypotenusen centimeter og vi ønsker å finne lengden av hosliggende katet. Om er lengden av hosliggende katet har vi at Da har vi at centimeter.
Vi definerer nå den siste av de tre grunnleggende trigonometriske funksjonene, tangens. Vi definerer Her må vi være forsiktige: hva om er null? Vi må fjerne disse verdiene fra definisjonsmengden. Vi vet at cosinus er null for de vinklene som som korresponderer til punkt på formen på enhetssirkelen, det vil si 90 og 270 grader, og alle omløp av disse. I radianer betyr dette at vi fjerner alle tall på formen hvor er et oddetall. Verdimengden er derimot alle reelle tall: når verdien av blir mindre vil verden av bli større.
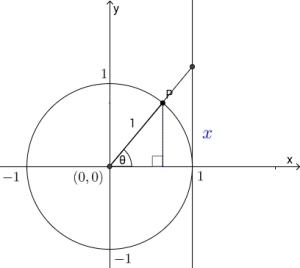
Om vi ønsker et geometrisk bilde av tangens, kan vi konstruere en rettvinklet trekant som er formlik den originale trekanten vår:
La være lengden av motstående katet i den store trekanten. Da denne er formlik den lille trekanten, er
Eksempel 3
Vi er gitt en rettvinklet trekant hvor en av vinklene er , lengden til hosliggende katet er centimeter, og vi ønsker å finne lengden til de to andre sidene. Merk at tangens gir oss
Vi har at . Dermed er lengden av motstående katet omtrent . Da kan vi finne lengden av hypotenusen ved hjelp av Pythagoras læresetning:
Del på Facebook
Lynkurs 11.-13.trinn
Trigonometri
Består av:
- Trekanter
- Sinus, cosinus og tangens
- Eksakte verdier
- Klara finner eksakte verdier
- Trigonometriske formler
- Grafene til sin x, cos x og tan x
- Arealsetningen
- Sinussetningen
- Cosinussetningen
- Trigonometriske likninger
- Mer kompliserte likninger
- Periodiske funksjoner
- Derivasjon av trigonometriske funksjoner
- Omskriving til standardform