Gitt en trekant  $ABC$ gir arealsetningen følgende formel for arealet av trekanten: $\frac{1}{2}\cdot AB\cdot AC\cdot \sin \angle A$. Ved å bruke andre sider av trekanten i formelen får vi tre formler for arealet, slik at

$$\frac{1}{2}\cdot AB\cdot AC\cdot \sin \angle A=\frac{1}{2}\cdot AB\cdot BC\cdot \sin \angle B=\frac{1}{2}\cdot AC\cdot BC\cdot \sin \angle C.$$

Om vi multipliserer hele uttrykket med $2$ får vi

$$AB\cdot AC\sin \angle A=AB\cdot BC\cdot \sin \angle A=AC\cdot BC\cdot \sin \angle C.$$

Om vi dividerer alt med $AB\cdot AC\cdot BC$ og forkorter, får vi: $\frac{\sin \angle A}{BC}=\frac{\sin \angle B}{AC}=\frac{\sin \angle C}{AB}.$

Eksempel 1

La $ABC$ være en trekant med $AB=3$, $\angle B={30}^{\circ }$ og $\angle C={80}^{\circ }$. Vi ønsker å finne sidelengdene $BC$ og $AC$. Sinussetningen gir $$\frac{AC}{\sin {30}^{\circ }}=\frac{3}{\sin {80}^{\circ }}.$$ Vi har at $\sin {30}^{\circ }=\frac{1}{2}$ og $\sin {80}^{\circ }\approx 0,98$. Da er $$\frac{AC}{0,5}=\frac{3}{0,98}.$$ Multipliserer vi alt med $0,5$ får vi at $AC\approx 1,53.$ For å finne $BC$ må vi vite vinkelen $\angle A$, men vi vet at summen av vinklene i en trekant er ${180}^{\circ }$, dermed er $\angle A={180}^{\circ }-{30}^{\circ }-{80}^{\circ }={70}^{\circ }.$ Da gir sinussetningen $$\frac{BC}{\sin {70}^{\circ }}=\frac{3}{0,98}.$$ Siden $\sin {70}^{\circ }\approx 0,94$ har vi at $BC\approx 2,88$.

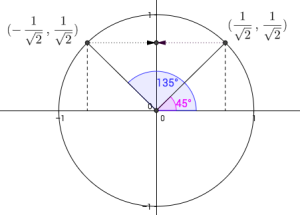
Om vi ønsker å bruke sinussetningen til å finne vinkler må vi være forsiktige. Husk at sinus av en vinkel $\theta$ er definert som $y$-koordinatet til det assosierte punktet på enhetssirkelen. Punktene $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ og $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ er begge på enhetssirkelen og har samme $y$-koordinat, men den rette linjen fra origo til disse punktene gir forskjellige vinkler, ${45}^{\circ }$ og ${135}^{\circ }$. Dermed er $$\sin {45}^{\circ }=\sin {135}^{\circ }.$$ Mer generelt har vi at $$\sin \theta =\sin ({180}^{\circ }-\theta )$$ for alle $\theta$. Tegn opp enhetssirkelen og sjekk selv! Av samme grunn har vi at $$\cos \theta =\cos ({360}^{\circ }-\theta ).$$

Eksempel 2

Vi er gitt en trekant $ABC$ med $\angle A={35}^{\circ }$, $AB=5$ og $BC=4$. Vi ønsker å finne vinklene ${\theta }_B$ og ${\theta }_C$, og lengden $AC$. Sinussetningen gir $\frac{\sin \angle C}{5}=\frac{\sin {35}^{\circ }}{4}.$ Dermed er $\sin \angle C\approx 0,72$. Taster vi inn ${\sin }^{-1}\left(0.72\right)$ på kalkulatoren, får vi at $\angle C\approx {46}^{\circ }$. Dermed kan vi finne $\angle B:$ $\angle B={180}^{\circ }-{35}^{\circ }-{46}^{\circ }={99}^{\circ }.$ Da kan vi finne $AC$ med sinussetningen: $$\frac{AC}{\sin {99}^{\circ }}=\frac{4}{\sin {35}^{\circ }}.$$ Dermed er $AC\approx 6,9$.

Men vi vet at $$\sin {46}^{\circ }=\sin {180}^{\circ }-{46}^{\circ }$$ og dermed ville det vært like riktig å velge $\angle C={180}^{\circ }-{46}^{\circ }={134}^{\circ }.$ Da får vi enda en løsning: $\angle B={180}^{\circ }-{134}^{\circ }-{35}^{\circ }={11}^{\circ }.$ Vi kan da bruke sinussetningen for å finne $AC$: $$\frac{AC}{\sin {11}^{\circ }}=\frac{4}{\sin {35}^{\circ }}.$$ I dette tilfellet dermed at $AC\approx 1,33$.

Eksempel 3

Vi er gitt en trekant $ABC$ med $\angle A={25}^{\circ }$, $AB=4$ og $BC=5$. Vi ønsker å finne vinklene $\angle B$ og $\angle C$ og lengden $AC$. Sinussetningen gir at $\frac{\sin {25}^{\circ }}{5}=\frac{\sin \angle C}{4}.$ Dermed er $\sin \angle C=\frac{4}{5}\sin {25}^{\circ }\approx 0,34.$ Om vi taster inn ${\sin }^{-1}(0,34)$ inn på kalkulatoren får vi omtrent $\angle C={20}^{\circ }.$ Da kan vi finne den manglende vinkelen $\angle B$: $\angle B={180}^{\circ }-{20}^{\circ }-{25}^{\circ }={135}^{\circ }.$ Da kan vi igjen bruke sinussetningen til å

finne den manglende siden $AC$:

$\frac{AC}{\sin {135}^{\circ }}=\frac{5}{\sin {25}^{\circ }}$

Dermed er $AC\approx 8,37$.

Men siden $\sin ({180}^{\circ }-\angle C)=\sin \angle C$ ville det vært like riktig å velge $\angle C={180}^{\circ }-{20}^{\circ }={160}^{\circ }$. Men dette går ikke! Vi vet at $\angle A={25}^{\circ }$, og ${160}^{\circ }+{25}^{\circ }={185}^{\circ }$. Da dette er større enn ${180}^{\circ }$ er ikke en slik trekant mulig. Dermed har vi funnet den unike løsningen.