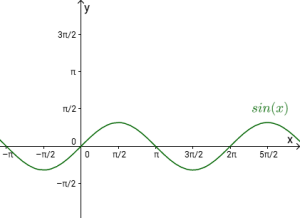
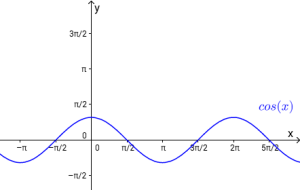
Grafene til sin x, cos x og tan x

Før vi ser på grafene til de grunnleggende trigonometriske funksjonene sin $u$, cos $u$ og tan $u$, husker vi først at vi bruker enhetssirkelen. Vinklene $u=\frac{\mathrm{\Pi }}{3}\left({60}^{\circ }\right)$, $u=\frac{5\mathrm{\Pi }}{2}\left({450}^{\circ }\right)$og $u=-\frac{\mathrm{\Pi }}{4}(-{45}^{\circ })$ lagt inn i hver sin enhetssirkel.

Definisjonen av trigonometriske funksjonene finner vi i artikkelen Sinus, cosinus og tangens.

Vi kan tegne grafene til de trigonometriske funksjonene på samme måte som vi tegner andre grafer: Ved å sette opp tabell og regne ut så mange funksjonsverdier som vi finner nødvendig for å tegne en jevn kurve. Vi kan derimot også bruker tabellen over eksakte verdier for sinus, cosinus og tangens i artikkelen Enhetssirkel.

Det er viktig at du kjenner utseendet på disse grafene godt. Her er noen huskeregler det er verdt å merke seg:

• $sin x$ går gjennom origo og går oppover derfra.

• $cosx$ er på en bølgetopp når $x=0$.

• $\sin x$ og $\cos x$ har verdimengden $[-1,1]$.

• Dersom grafen til $\cos x$ skyves $\frac{\pi }{2}$ enheter mot høyre, får vi grafen til $\sin x$.
  

• $\tan x$ går gjennom origo og går oppover derfra.

• Verdimengden til $\tan x$ er hele $ℝ$.

• $\tan x$ går mot pluss uendelig når $x$ nærmer seg verdiene $\pm \frac{\pi }{2},\pm \frac{3\pi }{2},\pm \frac{5\pi }{2},\mathrm{...}$  nedenfra, og mot minus uendelig når $x$ nærmer seg disse verdiene ovenfra. (Dette betyr at grafen har en vertikal asymptote for disse verdiene.)