Trekanter
Vi starter med litt notasjon og minner om de viktigste begrepene. Ved tegning av trekanter og andre mangekanter (eller
Polygon
Er det samme som en mangekant.
Se Mangekant.
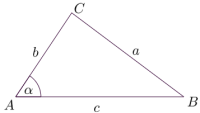
Vinkler betegnes gjerne med bokstavene og , eller greske bokstaver som . (Kan du uttale dem?) For å beskrive vinklene i en figur, bruker vi hjørnene til å veilede oss. På figuren over er for eksempel . Den midterste bokstaven betegner alltid toppunktet til vinkelen. I tilfeller der det ikke er noen tvil om hva vi mener, nøyer vi oss ofte med å skrive .
Spesielle trekanter
De grunnleggende egenskapene til disse trekant-typene kjenner du sikkert fra før: I en likesidet trekant er alle vinklene 60◦, mens i en likebeint trekant er det alltid to vinkler som er like store. For de rettvinklete trekantene gjelder et av de eldste og mest berømte av alle teoremer i matematikken, nemlig Pytagoras' setning.
Definisjon. spesielle trekanter
- En trekant der alle sidene er like lange, kalles likesidet.
- En trekant der to av sidene er like lange, kalles likebeint.
- En trekant der en av vinklene er rett, altså 90◦, kalles rettvinklet. Den motstående siden til den rette vinkelen kalles hypotenusen, mens de to andre er kateter.
Rettvinklet trekant
For de rettvinklete trekantene gjelder et av de eldste og mest berømte av alle teoremer i matematikken, nemlig
Pytagoras læresetning
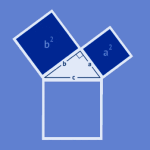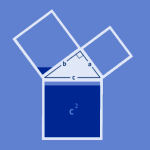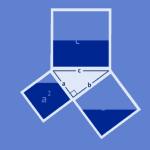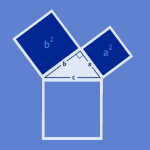
Pytagoras læresetning sier at:
Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.
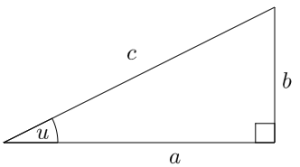
Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen :
Setningen kan brukes til å finne lengden til en side i en trekant.
Rettvinklet trekant med kateter a og b, og hypotenus c.
Det er viktig å merke seg at dersom sidelengdene i en trekant tilfredsstiller Pytagoras læresetning, så er trekanten rettvinklet. Fordi , er enhver trekant med sider rettviklet. Dette ble i gamle dager benyttet for å konstruere rette vinkler: Ta tre pinner med lengder , og lag en trekant med dem. Da får du en rettvinklet trekant!
30°, 60°, 90° - trekant
En annen god venn blant de rettvinklete trekantene er den der vinklene er 30°, 60° og 90°. En slik trekant kalles (oppfinnsomt nok) 30°, 60°, 90° - trekant.
teorem
Dersom den korteste kateten i en 30°, 60°, 90° - trekant har lengde , har vi at
- hypotenusen har lengde
- den lengste kateten har lengde
Bevis
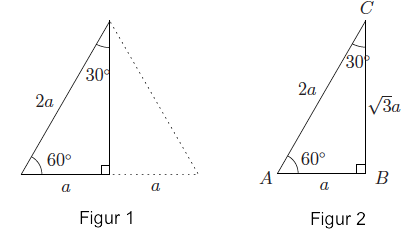
Ved å oppfatte 30°, 60°, 90° - trekant som halvparten av en likesidet trekant (figur 1), ser vi at hypotenusen har lengde . For å finne lengden av den andre kateten, bruker vi Pytagoras (figur 2):
Del på Facebook
Lynkurs 11.-13.trinn
Trigonometri
Består av:
- Trekanter
- Sinus, cosinus og tangens
- Eksakte verdier
- Klara finner eksakte verdier
- Trigonometriske formler
- Grafene til sin x, cos x og tan x
- Arealsetningen
- Sinussetningen
- Cosinussetningen
- Trigonometriske likninger
- Mer kompliserte likninger
- Periodiske funksjoner
- Derivasjon av trigonometriske funksjoner
- Omskriving til standardform