Cosinussetningen

Husk at

Pytagoras læresetning

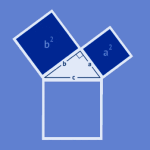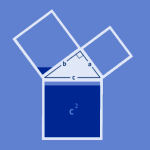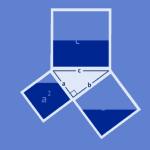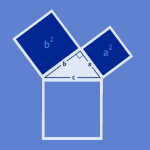
Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^2+b^2=c^2$ 

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras læresetning

$$h^2=a^2+b^2$$

hvor $h$ er lengden til hypotenusen og $a,b$ er lengden til katetene. Her skal vi utlede en formel som gjelder for vilkårlige trekanter.

Hvis trekanten er rettvinklet der $\angle A={90}^{\circ }$, så vet vi at $\cos {90}^{\circ }=0.$ I dette tilfellet er cosinussetningen den samme som Pytagoras læresetning: $$B{C}^2=A{C}^2+A{B}^2.$$ Merk også at cosinussetningen viser at de trekantene som oppfyller Pytagoras læresetningen, er nødvendigvis rettvinklet.

For å bruke sinussetningen må vi enten kjenne to vinkler og en motstående side, eller to sidelengder og en vinkel som ikke er vinkelen mellom de to sidene. Cosinussetningen gir oss dermed ny informasjon: om vi vet to sidelengder og vinkelen mellom dem kan vi finne den siste sidelengden. Om vi har alle tre sidene, kan vi også finne vinklene i trekanten.

Eksempel 1

I trekanten $ABC$ er $AB=4$, $AC=5$ og $\angle A={45}^{\circ }$. Vi ønsker å finne sidelengden $BC$ og vinklene $\angle B$ og $\angle C$. Vi kan finne sidelengden $BC$ ved cosinussetningen: $$B{C}^2=4^2+5^2-2\cdot 4\cdot 5\cdot \cos {45}^{\circ }\approx 12,72.$$ Da får vi at $BC\approx 3,57$. Nå kan vi bruke cosinussetningen til å finne $\angle B$: $$5^2=4^2+(3,57{)}^2-2\cdot 4\cdot (3,57)\cdot \cos \angle B.$$ Da får vi at $\cos \angle B\approx 0,13$. Taster vi inn ${\cos }^{-1}(0,13)$ på kalkulatoren vår får vi at $\angle B\approx 82,{53}^{\circ }.$ Da kan vi finne $\angle C$ ved å bruke at summen av vinklene i en trekant er ${180}^{\circ }$: $$\angle C={180}^{\circ }-{45}^{\circ }-82,{53}^{\circ }=52,{47}^{\circ }.$$ Vi kan sette prøve på svaret ved å finne $\angle C$ ved hjelp av cosinussetningen: $$4^2=5^2+(3,75{)}^2-2\cdot 5\cdot (3,75)\cdot \cos \angle C.$$ Da får vi at $\cos \angle C=0,675$. Taster vi inn ${\cos }^{-1}(0,675)$ på kalkulatoren får vi $\angle C=52,{05}^{\circ }$, som er omtrent det samme.

Ved bruk av sinussetningen er vi nødt til å ta hensyn til at det er to vinkler mellom $0^{\circ }$ og ${180}^{\circ }$ der sinus gir samme verdi. Dette er ikke et problem med cosinus: for alle tall $a$ i intervallet finnes det en entydig vinkel $\theta$ mellom $0^{\circ }$ og ${180}^{\circ }$ slik at $\cos \theta =a$. Dette kan du sjekke selv ved å tegne opp enhetssirkelen, for så å merke at for to forskjellige punkter i de to første kvadrantene må $x$-koordinatene også være forskjellige. Det samme kan vi ikke si om sinus: om du speiler punktet om $y$-aksen får du samme sinusverdi. (Du vil selvsagt få samme cosinusverdi om du speiler om $x$-aksen, men da havner du utenfor de to første kvadrantene.)

Eksempel 2

Vi er gitt en trekant $ABC$ med sidelengder $AB=3$, $BC=4$, $AC=5$. Vi ønsker å finne vinklene $\angle A,\angle B$ og $\angle C$. Vi finner først $\angle A$. Ifølge cosinussetningen er

$$4^2=3^2+5^2-2\cdot 3\cdot 5\cdot \cos \angle A.$$

Dermed er $\cos \angle A=\frac{3}{5}$, så $\angle A=53,{13}^{\circ }$. Vi finner nå $\angle B$:

$$5^2=4^2+3^2-2\cdot 3\cdot 4\cdot \cos \angle B.$$

Da har vi at $\cos \angle B=0$, slik at $\angle B={90}^{\circ }$. Da kan vi finne den siste vinkelen ved

$$\angle C={180}^{\circ }-{90}^{\circ }-53,{13}^{\circ }=36,{87}^{\circ }.$$