Hypergeometriske forsøk

Et hypergeometrisk forsøk har følgende egenskaper:

1. Det er totalt n gjenstander av to (eller flere) typer. 
2. Antallet gjenstander av type 1 er $n_1$ og antallet gjenstander av type 2 er $n_2$, slik at $n_1+n_2=n\mathrm{.}$
3. Det skal trekkes et uordnet utvalg uten tilbakelegging av størrelse k.

Det som interesserer oss er sannsynligheten for at det blir akkurat $k_1$ gjenstander av type 1 og $k_2$ gjenstander av type 2, hvor $k_1+k_2=k\mathrm{.}$ 

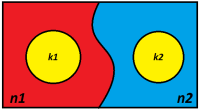
Bildet over illustrerer godt hvordan et hypergeometrisk forsøk fungerer. Det røde området betegner alle elementer av type 1 og det blå av type 2. Til sammen utgjør de alle de n gjenstandene. De to gule sirklene markert med $k_1$ og $k_2$ er antall objekter som skal trekkes fra henholdsvis type 1 og 2.

For hypergeometriske forsøk gjelder følgende regel:

Nå skal vi se på et par eksempler.

Kundeevaluering

Bildet er hentet fra www.psykiskhelsearbeid.no/ handbok_evaluering/

En dagligvarebutikk har gjennomført en undersøkelse blant kundene. 12 av kundene som deltok er misfornøyde. Blant disse er det åtte kvinner og fire menn. Butikksjefen ønsker å velge ut tre tilfeldige kunder blant de misfornøyde for å få mer informasjon om hva de ville forbedret. Hva er sannsynligheten for at det blir to kvinner og én mann?

Antall måter å trekke to kvinner på er

 $\left(\begin{array}{c}8\\ 2\end{array}\right)=\frac{8\cdot 7}{2}=28.$ 

Det er

 $\left(\begin{array}{c}4\\ 1\end{array}\right)=\frac{4}{1}=4$ 

måter å trekke ut en mann. Det finnes i alt

$\left(\begin{array}{c}12\\ 3\end{array}\right)=\frac{12\cdot 11\cdot 10}{3\cdot 2\cdot 1}=220$ 

måter å trekke tre personer fra en mengde av 12 mennesker.

Sannsynligheten for at det blir to kvinner og en mann er da lik

 $\frac{\left(\begin{array}{c}8\\ 2\end{array}\right)\cdot \left(\begin{array}{c}4\\ 1\end{array}\right)}{\left(\begin{array}{c}12\\ 3\end{array}\right)}=\frac{28\cdot 4}{220}=0,51$.

Frukt til tur

Karoline skal ha med frukt til en gåtur i skogen. Hun skal ta med fem stykker, og har så dårlig tid at hun bare drar med seg noen fra en kasse hun har stående. I kassen er det 10 pærer og 20 epler. Hva er sannsynligheten for at hun tar med seg tre pærer og to epler?

Dette er et hypergeometrisk forsøk siden Karoline skal trekke 5 frukter og har to ulike typer.

Vi har at $n_1=10,n_2=20,n=n_1+n_1=30,k_1=3,k_2=2$ og $k=k_1+k_2=5.$

Sannsynligheten for at Karoline velger 3 pærer og 2 epler er

 $\frac{\left(\begin{array}{c}10\\ 3\end{array}\right)\cdot \left(\begin{array}{c}20\\ 2\end{array}\right)}{\left(\begin{array}{c}30\\ 5\end{array}\right)}=\frac{120\cdot 190}{142506}=0,16$.