Betinget sannsynlighet og produktsetningen
Hva er betinget sannsynlighet, og hvordan regner vi med det?
Uttrykket betinget sannsynlighet brukes når sannsynligheten for en hendelse A påvirkes av om en annen hendelse B inntreffer. Vi sier at A og B er avhengige hendelser. Hvis sannsynligheten for A ikke påvirkes av B sier vi at de er uavhengige hendelser.
Vi bruker symbolet for hendelsen "A gitt B", og for sannsynligheten til en hendelse A forutsatt at hendelsen B allerede har inntruffet.
FORMEL FOR BETINGET SANNSYNLIGET
Hvis vi multipliserer med på begge sider av likhetstegnet, får vi
.
Dette uttrykket kalles produktsetningen.
PRODUKTSETNINGEN
hvor er den sannsynligheten for at inntreffer gitt .
Legg merke til at hvis A og B er uavhengige hendelser er , og da er , akkurat som vi lærte på ungdomsskolen.
Nå skal vi se på et par eksempler.
Russ og russebil
Sannsynligheten for at en elev i tredje klasse blir russ er 95%. Sannsynligheten for at eleven både blir russ og spleiser på en russebil er 15%. Hva er sannsynligheten for at eleven spleiser på en russebil når vi vet at hun er en russ?
Først innfører vi hendelsene
|
R: Eleven er russ |
B: Eleven spleiser på en russebil
|
Ut fra opplysningene vet vi at og . Dermed er
Sannsynligheten for at en russ spleiser på en russebil er omtrent 16%.
Gymtimer.
Idrettsstudenten Josefine har gjennomført en undersøkelse i en klasse med 20 elever, hvor av åtte er jenter. Elevene ble spurt om de liker gymtimene. Fem av jentene, og alle guttene, svarte ja. Josefine trekker en tilfeldig elev til et intervju. La J stå for at eleven er en jente og L for at eleven liker gymtimer.
Hvordan tolkes og , og hvor store er de?
- er sannsynligheten for at eleven er ei jente: .
- er sannsynligheten for at eleven liker gymtimer: .
- er sannsynligheten for at det er ei jente gitt at eleven liker gymtimer: . Legg merke til at her er utfallsrommet endret til elever som liker gymtimer i stedet for alle elevene! Det er 12 gutter og 5 jenter som liker gymtimer.
- er sannsynligheten for at eleven er ei jente og samtidig liker gymtimer: .
- er sannsynligheten for at eleven liker gymtimer gitt at det er ei jente:
Del på Facebook
Lynkurs 11.-13.trinn
Sannsynlighet (del II)
Består av:
- Repetisjon av begreper
- Hvordan finner vi uniform sannsynlighet?
- Venn-diagram og mengdelære
- Addisjonssetningen
- Sannsynlighet ved komplementære hendelser
- Betinget sannsynlighet og produktsetningen
- Bayes-setningen
- Uavhengige hendelser og produktsetningen
- Ikke-uniforme sannsynlighetsmodeller
- Ordnede utvalg
- Uordnede utvalg uten tilbakelegging
- Binomiske forsøk
- Hypergeometriske forsøk
Begrep
-
Betinget sannsynlighet
Den betingede sannsynligheten er sannsynligheten for en hendelse A forutsatt (gitt) at hendelsen B har inntruffet.
.
-
Produktsetningen
Produktsetningen sier at , hvor er den sannsynligheten for at A inntreffer gitt B.
-
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1. -
Snitt
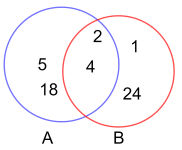
Snittet av to mengder A og B er en ny mengde som består av alle elementer som forekommer både i A og B.
Eksempel:
-
Uavhengige hendelser
To begivenheter A og B kalles uavhengige dersom utfallet i den ene ikke påvirker utfallet i den andre.
-
Utfall
Mulig resultat av en hendelse.
Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.
-
Utfallsrom
Alle mulige utfall en hendelse kan ha. Utfallsrom betegnes med .
Eksempel: Karakterer på en matematikkprøve har utfallsrommet .




