Hopp til hovedinnholdet
www.matematikk.org

Addisjonssetningen

En kombinert begivenhet er unionen av flere hendelser. Addisjonssetningen bruker vi når vi ønsker å finne sannsynligheten for en kombinert begivenhet. Setningen sier at vi finner sannsynligheten for en kombinert begivenhet ved først å legge sammen sannsynligheter for hver enkel hendelse for så å trekke fra sannsynligheter som er telt flere ganger (snittet av hendelsene).

ADDISJONSSETNING

 P(A∪B)=P(A)+P(B)−P(A∩B) 

 

Hvis A og B er to disjunkte hendelser, er P(A∩B)=0, hvilket medfører at

 P(A∪B)=P(A)+P(B). 

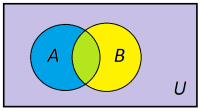
La oss illustrere addisjonssetningen med et Venn-diagram.

Unionen av A og B, A∪B, er det blå, grønne og gule området som er dekket av de to sirklene. Unionen skal være lik A+B−A∩B, fordi i A+B har vi tatt med det felles arealet A∩B to ganger (både i A og i B). Vi må med andre ord trekke fra summen av det grønne området for å kompensere. Hvis A og B er to disjunkte hendelser, har de ikke noe felles areal og derfor er A∪B=A+B.

Handletur uten handleliste

Den mest glemsomme i gjengen fikk ansvar for å ta med seg pålegg på hytteturen. Handlelisten bestod av gulost, brunost, kokt skinke, spekeskinke, smør og majones. Den glemsomme glemte å ta med handlelisten til butikken, og glemte én av tingene han skulle ha tatt med.

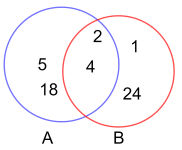
Vi antar at det er like stor sannsynlighet for at han glemmer hver av dem, og lar begivenheten A={gulost,skinke} være at han glemte å kjøpe gulost eller skinke, og B={skinke,majones} være at han glemte å kjøpe skinke eller majones. Hva er sannsynligheten for at han glemte enten ost, skinke eller majones, altså for et utfall i unionen A∪B?

Den enkleste måten å finne P(A∪B)=P⁢ ({ost,skinke,majones}) er å dele antall gunstige utfall på antall mulige, som er

 36=12=50%.

Vi kan også tenke oss fram til dette på en annen måte:

 P(A)=26=13, P(B)=26=13 og P(A∩B)=P⁢ ({skinke})=16.

I følge addisjonssetningen blir

 P(A∪B)=P(A)+P(B)−P(A∩B)=13+13−16=12=50%,

som er den samme som vi fikk ved den første løsningsmetoden.

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Sannsynlighet (del II)

Består av:

Begrep

  • Addisjonssetningen

    Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.

    P(A∪B)=P(A)+P(B)−P(A∩B)

  • Begivenhet

    En begivenhet er en delmengde av utfallsrommet og består av ett eller flere utfall.

    ·         Å få 6 på en terning er et eksempel på en begivenhet, der utfallsrommet består av 1, 2, 3, 4, 5 og 6. Å få høyere enn 3, altså 4, 5 eller 6, er et annet eksempel på en begivenhet.

  • Disjunkte hendelser

    A og B kalles disjunkte dersom de ikke har noen felles elementer. Dette betyr at A∩B=∅, altså at det ikke er noen elementer som er både i A og i B.

  • Sannsynlighet

    Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
    En sannsynlighet er minst 0 og maks 1.

    Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
    Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

    Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

    Sannsynligheten for å få mynt eller kron er 1.

  • Snitt

    Snitt

    Snittet av to mengder A og B er en ny mengde A∩B som består av alle elementer som forekommer både i A og B.

    Eksempel:

    A={2, 4, 5, 18} og B={1, 2, 4, 24}

    A∩B={2, 4}

  • Union

    Union

    Unionen av to mengder A og B er en ny mengde A∪B som består av alle elementer som forekommer i minst en av A og B.  

    Eksempel: hvis  A = 2, 4, 5, 18 og B = 1, 2, 4, 24 er to mengder, blir unionen A ∪ B = 1, 2, 4, 5, 18, 24. 

  • Utfall

    Mulig resultat av en hendelse.

    Eksempel: Du kaster en terning og får seks øyne. Utfallet er seks. Du kaster en mynt og får kron. Kron er utfallet.

Hopp over bunnteksten