Uavhengige hendelser og produktsetningen
Hva er uavhengige hendelser? Hvordan finner vi sannsynligheten for at flere uavhengige hendelser inntreffer samtidig?
To hendelser A og B kalles uavhengige om utfallet av den ene ikke påvirker utfallet av den andre. Sannsynligheten for at flere uavhengige hendelser inntreffer samtidig, er gitt som produktet av sannsynligheter for hver enkel hendelse.
PRODUKTSETNINGEN
Når to begivenheter A og B er uavhengige, har vi
Denne regelen bruker vi også andre veien noen ganger, når det er lett å finne de forskjellige P-ene i regelen: Hvis , er A og B to uavhengige hendelser.
Kinosaler
Bildet er hentet fra www.superman-picture.com
Kjetil bor i en by med to kinoer, M og N. Han vil se filmen "Superman" i en av de største salene. Sannsynligheten er 90% for at filmen vises i den største salen på kino M, mens den er 60% for at den vises i den største salen på kino N. Han vet også at det er 50% sannsynlighet for at filmen går på den største salen på begge kinoene. Er det at filmen vises i den største salen i en kino uavhengig av om den vises i den største salen i den andre?
La A stå for at filmen vises i den største salen på kino M og B at filmen vises i den største salen på kino N. Vi vet at
og .
Vi kan nå regne ut at , og dette er ikke det samme som . Fra regelen vet vi dermed at A og B ikke er uavhengige. Dette betyr at kinoenes valg av sal er påvirket av hva den andre velger.
Skolebussen
Bildet er hentet fra bfk.no
Emilies skolebuss er ofte forsinket. Det er 30% sannsynlighet for at bussen er forsinket om morgen og 20% om ettermiddagen. Emilie har lyst til å klage på dette, men først vil hun ha alle fakta og derfor ønsker hun å beregne sannsynligheten for at bussen kommer for sent både på vei til skolen (S) og på vei hjem fra skolen (H).
La betegne sannsynligheten for forsinkelsen om morgen og sannsynligheten for at bussen kommer for sent om ettermiddagen. Vi vet at og . I tillegg antar vi at forsinkelse fra og til skolen er to uavhengige begivenheter, siden det er to forskjellige sjåfører som kjører om morgen og om kvelden.
Derfor er sannsynligheten for at skolebussen kommer for sent både om morgen og om ettermiddagen lik produktet av de to sannsynlighetene:
.
Dette betyr at skolebussen er forsinket både morgen og kveld cirka hver 17. dag, altså litt sjeldnere enn hver tredje uke i snitt.
Kan du bruke regnereglene for komplementære hendelser og finne sannsynlighetene og ? Hva betyr de i praksis?
Del på Facebook
Lynkurs 11.-13.trinn
Sannsynlighet (del II)
Består av:
- Repetisjon av begreper
- Hvordan finner vi uniform sannsynlighet?
- Venn-diagram og mengdelære
- Addisjonssetningen
- Sannsynlighet ved komplementære hendelser
- Betinget sannsynlighet og produktsetningen
- Bayes-setningen
- Uavhengige hendelser og produktsetningen
- Ikke-uniforme sannsynlighetsmodeller
- Ordnede utvalg
- Uordnede utvalg uten tilbakelegging
- Binomiske forsøk
- Hypergeometriske forsøk
Begrep
-
Komplement
Komplementet til A, betegnet med , består av alle elementer som er i utfallsrommet U men ikke i A. Med andre ord, .
-
Sannsynlighet
Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.
Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.
Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.
Sannsynligheten for å få mynt eller kron er 1. -
Snitt
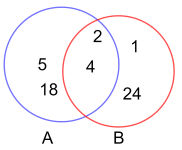
Snittet av to mengder A og B er en ny mengde som består av alle elementer som forekommer både i A og B.
Eksempel:
-
Uavhengige hendelser
To begivenheter A og B kalles uavhengige dersom utfallet i den ene ikke påvirker utfallet i den andre.






