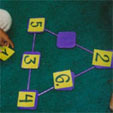
Magiske figurer

Utstyr

tynn papp/ papir
papir og blyant

Magisk trekant Magisk kvadrat

I snekkerboden - utstyret blir til

Lag 9 tallkort med alle heltallene fra 1 til 9 (se vedlegg ”tallkort”).

Magiske trekanter

Kopier opp trekantmaler (se vedlegg). Disse trekantmalene kan lages i stivere papp eller eventuelt ved hjelp av trebrikker som limes på trepinner. Da får du stativer som er mer holdbare, og som kan brukes gjentatte ganger. Se bildet øverst på siden.

Magiske kvadrat
På samme måte som med trekantmalen lager du et kvadrat bestående av 3 x 3 mindre like store kvadrater. Dette skal bli et magisk kvadrat. En kan også her velge å lage kvadratet ved hjelp av trebrikker og trepinner.

Matematikken i aktiviteten

Magiske trekanter
Til å begynne med skal bare de seks første tallkortene brukes. Da blir hovedoppgaven å plassere tallene fra 1 til 6 langs sidene i trekanten (fra trekantmalen), slik at summen er den samme langs hver side av trekanten.

Når denne oppgaven er løst kan en se på:
-    Hvilke ulike muligheter finnes for summen?
-    Hvordan kan dere vite om dere har funnet alle løsningene?
-    Finner dere et system?
-    Hva skjer om dere bruker tallkortene fra 2 til 7 i stedet? - eller fra 3 til 8? Gjett først hvilke summer som er mulig.

Videre kan en tenke over:
-    Hva er den minste summen som er mulig? Hvorfor?
-    Hva er den største summen som er mulig? Hvorfor?
-    Hvilke mønster ser dere for de ulike summene?

Magiske kvadrat
Et magisk kvadrat består av små kvadrater satt sammen til et større kvadrat, der hvert lille kvadrat inneholder et tall og tallene er plassert etter et bestemt mønster. Summen av tallene langs hver horisontale, vertikale og diagonale linje er den samme. Denne summen kalles ”Den magiske summen”.

Løsningen på det enkleste magiske kvadratet der en bruker tallene fra 1 til 9 er å putte partallene i hjørnene, 5-tallet i midten og de andre oddetallene på sidene. Her er den magiske summen 15. La dette være den første oppgaven til elevene. Presenter for dem hva et magisk kvadrat er, og utfordre dem til å fylle ut kvadratet på 3 x 3 ruter. Videre kan en prøve å få dem til å tenke over hvorfor den magiske summen er 15.

Hvordan differensiere?

Her er det virkelig rom for differensiering. Magisk trekant med små tall er lettere enn magisk kvadrat med små tall. En kan også utvide med å bruke andre tall, for eksempel partallene fra 2 til 20 i stedet for tallene 1 - 9. Hva skjer da? For ytterligere ideer, se undervisningsoppleggene "Magiske kvadrat" og "Magiske trekanter".