Magiske kvadrater

 

Skilpadden som kom opp av elva.

Legenden om Lo Chu ble funnet i Kina i en bok med tittel Yih King, og i en litt forkortet versjon går legenden omtrent sånn: I Kina var det for lenge siden en stor flom. Folk prøvde å ofre til "elveguden" i elva Lo for å stagge hans sinne. Hver gang kom det en skilpadde opp av elva og vandret rundt offeret før den gikk tilbake til elva. Elveguden aksepterte ikke offeret, og flommen fortsatte. Dette gjentok seg inntil et lite barn skjønte den kuriøse figuren på skilpaddeskallet. Det forestilte et magisk kvadrat som skrevet på en litt ryddigere måte ser slik ut: 

4	9	2
3	5	7
8	1	6

Summen i hver rad, hver søyle og de to diagonalene er alle 15. Da skjønte kineserene at det rette antallet ofre var 15, og de klarte å stagge elveguden.

Definisjon av magisk kvadrat
En oppstilling av de naturlige tallene fra 1 til n² i n rekker og n kolonner med følgende egenskap: Summen av tallene i hver rekke, hver kolonne og langs hver diagonal er den samme.

Tallet n kalles kvadratets orden. Skilpaddeskallet er altså et magisk kvadrat av tredje orden.

Et uløst matematisk problem er å finne antallet av mulige kvadrater av en gitt orden. Når man ser bort fra dreininger og rotasjoner, finnes det kun én type kvadrat av tredje orden og 880 av fjerde orden. Antallet femte ordens kvadrater er ikke kjent, men er trolig over 13 millioner.

Den magiske summen for et magisk kvadrat av orden m er gitt ved $S=\frac{m(1+m^2)}{2}$, det vil si at for m=3 har vi $S=\frac{3(1+9)}{2}=15$, mens vi for m=4 har $S=\frac{4(1+16)}{2}=34$.

De magiske kvadratene av tredje orden har i utgangspunktet 9 ukjente:

 

a	b	c
d	e	f
g	h	i

Summen i hver rad, kolonne og diagonal skal være 15, noe som gir oss 8 likninger å løse. Noen av disse er overflødig,e og etter noe regning ender vi opp med følgende kvadrat som gir oss alle løsninger

 

a	b	15-a-b
20-2a-b	5	-10+2a+b
-5+a+b	10-b	10-a

Nå kan vi sette inn verdier for a og b. Det er i alt 8 mulige:

a	2	2	4	4	6	6	8	8
b	7	9	3	9	1	7	1	3

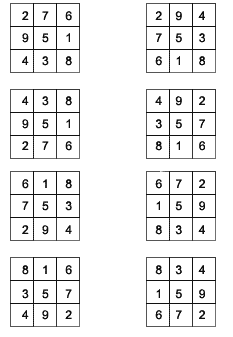
Setter vi inn verdiene i kvadratet får vi følgende 8 magiske kvadrater:

 

De 8 ulike magiske kvadratene.

og det er enkelt å se at disse essensielt er samme kvadrat, bare rotert eller speilet.

For et magisk kvadrat av orden 4 har vi tilsvarende 16 ukjente, og vi har 9 uavhengige betingelser, noe som gir oss 7 parametre. Ikke alle valg av verdier for disse parametrene gir oss ekte kvadrater, for å være nøyaktig er tallet 7 040. Men så er det også her mange overflødige, det vil si noen magiske kvadrater som vi kan lage fra andre ved rotasjoner eller andre symmetrier.

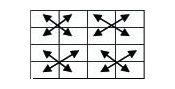
For hvert magisk kvadrat har vi 4 rotasjoner og 2 speilinger, noe som gir oss 8 "stive" symmetrier. I tillegg har vi noe vi kan kalle "aritmetrier", der vi beholder alle de 8 regnestykkene (4 rader, 4 søyler og 2 diagonaler) i kvadratet, men forandrer geometrien. Vi har flere typer aritmetrier:

 

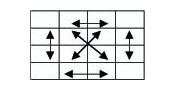
og denne

 

Et par eksempler på magiske kvadrater av orden 4:

 

9	4	5	16
15	10	3	6
2	7	14	11
8	13	12	1

og dets aritmetiske komplement, som i dette tilfellet er en speiling om horisontalen. Det aritmetiske komplement til et kvadrat lager vi ved å ta én mer enn det største tallet og trekke fra tallet i hver rute. Én mer enn 16 er 17 og 17 - 9 = 8, 17 - 4 = 13, osv.

 

8	13	12	1
2	7	14	11
15	10	3	6
9	4	5	16

Dette kvadratet er en aritmetri av kvadratet over:

 

7	2	11	14
13	8	1	12
4	9	16	5
10	15	6	3

Et annet eksempel på et magisk kvadrat av orden 4:

 

6	2	11	15
7	13	4	10
9	3	14	8
12	16	5	1

og dets aritmetiske komplement som i dette tilfellet ikke er en symmetri:

 

11	15	6	2
10	4	13	7
8	14	3	9
5	1	12	16

Vi har altså aritmetiske komplementer som er symmetrier, og noen som ikke er symmetrier.