Bestemte integraler

Vi begynner med definisjonen av et bestemt integral.

Her ser vi sammenhengen mellom et bestemt og et ubestemt integral. I forrige del lærte vi å beregne antideriverte til en funksjon, og nå ser vi en måte å bruke dem på. Merk at på høyresiden blir konstanten $C$ borte i subtraksjonen, så når vi skal regne ut bestemte integraler trenger vi ikke å prøve å finne den.

Hva er det bestemte integralet? En av de viktigste tolkningene er at det er en arealberegning:

Eksempel

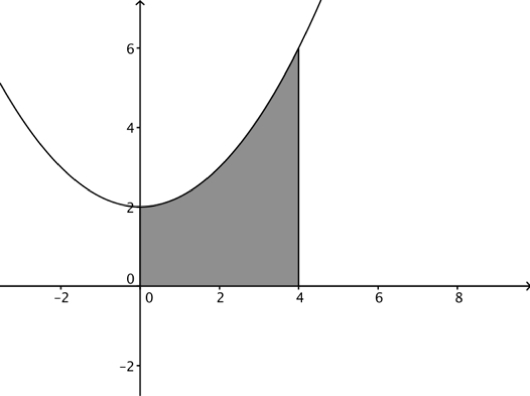
Oppgave. Hva er arealet under grafen til $f\left(x\right)=\frac{1}{4}{x}^2+2$, og mellom 0 og 4 på $x$-aksen? (Se bildet nederst på siden)

Løsning. I følge teoremet over trenger vi en antiderivert, og med regnereglene fra forrige seksjon ser vi at

${\int }_{}^{}f\left(x\right)\mathrm{dx}={\frac{1}{12}x}^3+2x+C$.

Da kan vi bruke teoremet, og gjøre denne utregningen:

${\int }_0^{4}f\left(x\right)\mathrm{dx}={\frac{1}{12}\cdot 4}^3+2\cdot 4-\left({\frac{1}{12}\cdot 0}^3+2\cdot 0\right)=\frac{40}{3}$.

Arealet av det skraverte området på bildet er dermed $\frac{40}{3}$. Siden vi ikke har noen enheter i oppgaveteksten kan vi ikke gi noen måleenhet her.

I GeoGebra-arket under kan du prøve å flytte grenser og endre funksjon og se hvordan integralet ser ut. Hva skjer med det bestemte integralet hvis funksjonen også er negativ? Prøv å regne ut integralet av $f\left(x\right)=x^3$ fra $-1$ til $1$. Hva ser du da?

Bestemt integral