Andregradsfunksjoner

Vi har sett på lineære funksjoner, der variabelen er i første potens. Nå skal vi se på hva som skjer hvis vi har variabelen i andre potens. Vi får da det vi kaller en kvadratisk funksjon, eller andregradsfunksjon.

La oss starte med å klargjøre hva vi mener med en andregradsfunksjon. En lineær funksjon, eller en førstegradsfunksjon, ser slik ut:

$y = a x + b$ .

Nå vil vi ha et ledd til, der $x$ er i andre potens, og en andregradsfunksjon ser slik ut:

$y = a x^{2} + b x + c$ .

Her er a, b og c vilkårlige tall. Merk at hvis $a = 0$ er funksjonen bare en lineær funksjon. Konstantene a, b og c gir oss mye informasjon om hvordan grafen til funksjonen ser ut. Vi går gjennom noen regler.

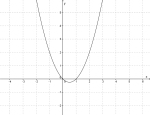
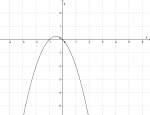
Konstanten a

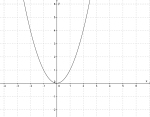
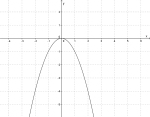
Fortegnet foran $a$ forteller oss om grafen er bøyd oppover eller nedover.
Når $a > 0$ bøyer grafen seg oppover.
Når $a < 0$ bøyer grafen seg nedover.
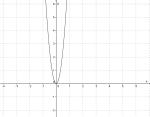
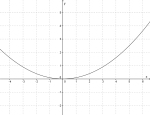
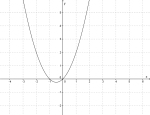
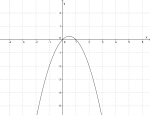
Når $a$ er et stort tall er funksjonen bratt, og når $a$ er et lite tall blir den slak.
Når $a = 10$ er grafen til funksjonen allerede mye brattere.
Når $a = \frac{1}{10}$ er grafen til funksjonen allerede mye slakere.

Konstanten b

Fortegnet foran $b$ forteller oss hvordan grafen er forskjøvet langs $x$ -aksen.

Dersom $a$ er positiv og $b$ er negativ, er grafen flyttet mot høyre, og bunnpunktet er på høyre side av $y$ -aksen.
Dersom $a$ er positiv og $b$ er positiv, er grafen flyttet mot venstre, og bunnpunktet er på venstre side av $y$ -aksen.
Dersom $a$ er negativ og $b$ er negativ, er grafen flyttet mot venstre, og topp-punktet er på venstre side av $y$ -aksen.
Dersom $a$ er negativ og $b$ er positiv, er grafen flyttet mot høyre, og topp-punktet er på høyre side av $y$ -aksen.

Konstanten c

Tallet $c$ forteller oss hvor grafen skjærer $y$ -aksen. Her kan vi tenke som for lineære funksjoner: Når grafen skjærer $y$ -aksen er $x = 0$ , så da er $y = c$ , og dermed får vi følgende regel:

Grafen krysser y-aksen i $c$ , uavhengig av fortegnet til $c$ .
Når $c = 2$ krysser grafen $y$ -aksen i $2$ .
Når $c = - 2$ krysser grafen $y$ -aksen i $- 2$ .

Del på Facebook

Del på Facebook

Lynkurs, 8.-10.trinn

Funksjoner (del I)

Består av:

Begrep

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.
Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$
Variabel

En bokstavbetegnelse på et vilkårlig element i en mengde. Det motsatte er en konstant.

Eksempel: I uttrykket y = x + 3 er 3 en konstant og x en variabel. y er en annen variabel, avhengig av x.

Se Variable størrelser

Andregradsfunksjoner

Konstanten a

Konstanten b

Konstanten c

Lynkurs, 8.-10.trinn

Funksjoner (del I)

Består av:

Begrep

Andregradsuttrykk

Graf

Ligning

Variabel

Se