Fra en graf til en funksjon
Hvordan kan vi finne funksjonsuttrykket som gjemmer seg bak en graf? Vi har sett på hvordan man kan gå fra en funksjon til en graf, men noen ganger vil man også gå andre vei. Det er ikke alltid åpenbart, men når man vet om noen typer funksjoner kan man prøve ut om noen av dem kan passe.
Husk her at punktene på en graf er tallpar som har en -verdi og -verdi. Vi skriver dem med -verdien først, og -verdien sist.
Vi skal vise hvordan man gjør dette ved hjelp av noen eksempler. Hvis du derimot ønsker å teste deg selv, utfordrer vi deg med denne oppgaven:
Eksempel 1
Finn funksjonen til denne grafen:
Vi ser vi på grafen og velger et par punkter som ligger på grafen. Punktene er tallpar , og verdiene finner vi ved å lese av aksene. I bildet under, for eksempel, finner vi koordinatene til det blå punktet lengst til høyre ved å gå ned til -aksen og bort til -aksen og lese av verdiene. Dette punktet er .
For å få oversikt over punktene, lager vi en verditabell med de valgte punktene.
Klarer vi nå å se et mønster? Vi ser at når , er halvparten så stor. Hvis vi ser på de andre verdiene, stemmer dette ganske bra. Vi kan konkludere med at hver blir halvert, altså er funksjonsuttrykket .
Eksempel 2
Finn funksjonen til denne grafen:
Det første vi gjør er å velge ut noen punkter som ligger på grafen. Her kan vi for eksempel velge punktene .
Vi setter opp en verditabell med disse punktene.
Vi kan prøve å finne funksjonen nå. Det ser ut til at vi regner ut fra ved å multiplisere med (Regn over og sjekk at dette er sant). Da tror vi at funksjonen til grafen er . Hvis du prøver å tegne denne funksjonen vil du se at det er den samme som vi har tegnet over.
Eksempel 3
Nå skal vi se på en litt mer krevende funksjon. Finn funksjonen til denne grafen:
La oss først velge ut noen punkter som ligger på grafen, som for eksempel . Disse setter vi så inn i en verditabell:
Klarer vi å finne et mønster? Det første punktet sier at når , er . Dette forteller oss at 5 trekkes fra . Vi gjetter på at funksjonsuttrykket er . Setter vi inn -verdiene fra tabellen, skal vi få de tilhørende -verdiene fra tabellen:
Vi ser at dette ikke stemmer. -verdiene vi får er ikke de samme som er i verditabellen. Dette betyr at vi ikke har riktig funksjonsuttrykk.
Siden det første punktet forteller oss at 5 trekkes fra, er dette greit. Men dette betyr at noe mer blir gjort med verdien vi setter inn for . Kan det være at for eksempel denne verdien blir doblet før 5 trekkes fra? Vi gjetter nå at funksjonsuttrykket er . Setter vi inn -verdiene fra tabellen, skal vi få de tilhørende -verdiene fra tabellen:
Vi ser at dette stemmer godt med verditabellen. Da har vi funnet funksjonsuttrykket!
Dette eksemplet viser at det kan være vanskelig å finne funksjonsuttrykket bare ved å se på grafen og lage en verditabell. Det er ikke alltid enkelt å se et mønster. Derfor finnes det andre lure metoder for å finne et funksjonsuttrykk. Alle våre eksempler har vært rette linjer. For å finne funksjonsuttrykket for en rett linje på en lur måte, se i høyrespalten.
Del på Facebook
Lynkurs, 8.-10.trinn
Funksjoner (del I)
Består av:
- Hva er en funksjon?
- Koordinatsystem
- Fra en funksjon til en graf
- Rette linjer (lineære funksjoner)
- Proporsjonalitet
- Fra en graf til en funksjon
- Andregradsfunksjoner
- Funksjonsgrafer for andregradsfunksjoner
- Hvorfor ser grafen ut som den gjør?
- Inger Christin forteller om funksjoner.
- Test deg selv i lineære funksjoner!
- Test deg selv i funksjoner!
Begrep
-
Akse
Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
-
Brøk
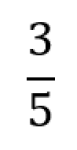
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
-
Koordinatsystem
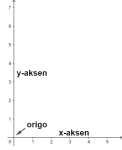
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
-
Verditabell
En tabell med verdier av en variabel, for eksempel , og tilhørende funksjonsverdier, for eksempel , kalles for en verditabell.
Verditabellen gir oss oversikt over verdier som hører sammen. Den hjelper oss enten med å finne punkter som ligger på grafen til en funksjon eller funksjonsuttrykket til en graf.
-
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse. -
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.









