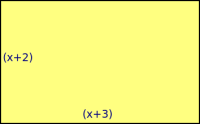Andregradslikninger

Hva er en andregradslikning?

Andregradslikninger er likninger der den ukjente har 2 som største eksponent. Denne typen likninger er på formen ${a x}^{2} + b x + c = 0$ , der $x$ er den ukjente og $a \neq 0$ . Både $b$ og $c$ kan være lik 0. La oss se hvordan andregradslikninger kan se ut:

1.	$a x^{2} = 0$	$b = c = 0$
2.	$a x^{2} + c = 0$	$b = 0$
3.	$a x^{2} + b x = 0$	$c = 0$
4.	$a x^{2} + b x + c = 0$

Eksempler

$3 x^{2} = 0$
$4 x^{2} + 7 = 0$
$5 x^{2} + 3 x = 0$
$x^{2} + 6 x + 9 = 0$
$y^{2} = 9$
$z^{2} - 9 z = 0$

Legg merke til at i 5. er den ukjente $y$ og på høyresiden av likhetstegnet står det ikke 0. Dette er fortsatt en andregradslikning, fordi vi kan trekke fra 9 på begge sider av likningen. Da vil likningen se ut som $y^{2} - 9 = 0$ . Legg ogås merke til at i 6. heter den ukjente $z$ . Husk at vi kan den ukjente kan være hvilken som helst bokstav.

Geometrisk tolkning

Andregradslikninger kan ofte bli tolket geometrisk. En andregradslikning som for eksempel

$(x + 2) (x + 3) = 20$

er et produkt av to faktorer. Dette uttrykket kan vi derfor tolke som spørsmålet:

Hvor stor er $x$ hvis arealet av rektangelet med lengde $l = (x + 2)$ og bredde $b = (x + 3)$ er $20$ ?

Vi kan løse andregradslikningen ved å få den på den generelle formen og bruke abc-formelen. Eller vi kan prøve å tegne forskjellige figurer, mutliplisere sammen lengden og bredden og se når arealet er $20$ . Hvis vi prøver $x = 2$ , får vi en løsning.

Hvis vi løser andregradslikningen ved hjelp av abc-formelen, vil vi få $x = - 7$ som den andre løsningen. Denne løsningen ser vi bort ifra, fordi det ikke gir mening at lengden eller bredden til en rektangel er negativ.

Del på Facebook

Del på Facebook

Tilsvarende emner behandles også i

Løs en andregradslikning.

Begrep

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.
Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger
Komplekse tall

Komplekse tall er en utvidelse av de reelle tall. De er satt sammen av en realdel og en imaginærdel. Tallene kan fremstilles i et tallplan hvor førsteaksen er de reelle tallene og andreaksen de imaginære tallene. Den imaginære enheten er $i = \sqrt{- 1}$ . Et komplekst tall angis ofte på formen a + ib, hvor a og b er reelle tall.
Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$
Tallinje

En rett linje der hvert punkt korresponderer til et tall og ethvert tall svarer til et punkt på linjen.

Andregradslikninger

Eksempler

Geometrisk tolkning

Tilsvarende emner behandles også i

Begrep

Andregradsuttrykk

Eksponent

Komplekse tall

Ligning

Tallinje