Hvorfor ser grafen ut som den gjør?
Vi har sett at å tegne grafen til rette linjer er ganske rett (!) fram. For andregradsfunksjoner tegner vi en avrundet bue, men hvordan kan vi vite at det er sånn de skal se ut?
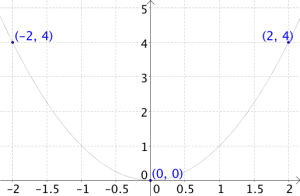
Her skal vi se på grafen til funksjonen . Sånn vi lærte å gjøre det velger vi noen -verdier, la oss si , og , og regner ut -verdiene som hører til. Da får vi følgende tabell:
| -2 | 0 | 2 | |
| 4 | 0 | 4 |
Hvis vi merker av disse tre punktene i et koordinatsystem og tegner en andregradsfunksjon gjennom dem får vi noe som dette:
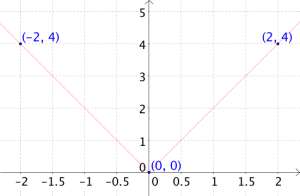
Dette kan se vel og bra ut, men hvis vi tenker på det litt kan det hende vi blir usikre. Hvordan vet vi at dette er riktig form på funksjonen? For eksempel kunne vi kanskje tegnet følgende:
Dette er ikke grafen til , men hvordan kan vi vite det? La oss prøve å ta med to punkter til i verditabellen vår, så den blir:
| -3 | -2 | 0 | 2 | 3 | |
| 9 | 4 | 0 | 4 | 9 |
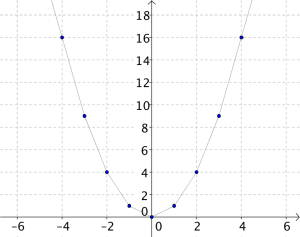
Vi tegner begge de to funksjonsgrafene vi hadde over og merker også av de to nye punktene:
Nå ser vi at den røde grafen ikke passer lenger, mens den første vi prøvde fortsatt treffer fint.
Hvis vi tar med enda flere punkter i verditabellen vår og tegner linjestykker mellom dem aner vi hvordan vi kunne oppdaget formen på hvis vi ikke visste det på forhånd:
Moralen er at hvis vi er usikre på hvordan en funksjon ser ut kan vi alltids prøve å lage en større verditabell.
Del på Facebook
Lynkurs, 8.-10.trinn
Funksjoner (del I)
Består av:
- Hva er en funksjon?
- Koordinatsystem
- Fra en funksjon til en graf
- Rette linjer (lineære funksjoner)
- Proporsjonalitet
- Fra en graf til en funksjon
- Andregradsfunksjoner
- Funksjonsgrafer for andregradsfunksjoner
- Hvorfor ser grafen ut som den gjør?
- Inger Christin forteller om funksjoner.
- Test deg selv i lineære funksjoner!
- Test deg selv i funksjoner!
Begrep
-
Andregradsuttrykk
Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.
-
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.