Funksjonsgrafer for andregradsfunksjoner

Eksempel 1

Dette er grafen til en andregradsfunksjon:

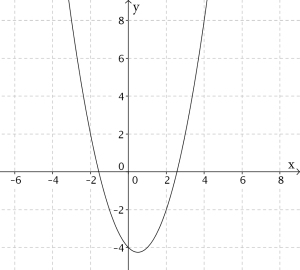
Vi ser her at grafen bøyer seg oppover, og derfor må $a$ være positiv. Siden $a$ er positiv og bunnpunktet er til høyre for $y$-aksen, må $b$ være negativ. Til slutt ser vi at grafen krysser $y$-aksen i punktet $(0,-4)$ og da må $c=-4$.

Vi har fått mye informasjon om funksjonen bare ved å se på grafen, og vi kan avsløre at dette er grafen til denne funksjonen:

$y=x^2-x-4$.

Sjekk gjerne at dette stemmer ved å sette inn noen verdier av $x$, og sjekk at du får riktige verdier for $y$.

Eksempel 2

Dette er grafen til en andregradsfunksjon:

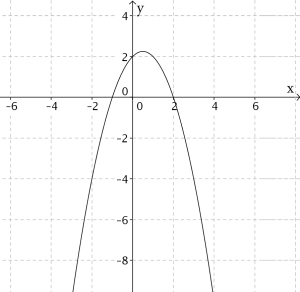
Her ser vi at grafen bøyer seg nedover, topp-punktet er til høyre for $y$-aksen, og den krysser $y$-aksen i punktet $(0,2)$.

Hva kan du si om $a$, $b$ og $c$? Klarer du å finne funksjonsuttrykket ved å se på grafen? Når du finner funksjonen, prøv å regne ut noen punkter på den for å se at du har truffet.

Eksempel 3

Vi vil skissere grafen til funksjonen $y=x^2+3x-5$.

Vi ser først at $a=1$, $b=3$ og $c=-5$. Siden $a$ er positiv, bøyer grafen oppover. Siden både $a$ og $b$ er positive, er grafens bunnpunkt til venstre for y-aksen. Til slutt ser vi at grafen krysser $y$-aksen i punktet $(0,-5)$ siden $c=-5$.

Skissér grafen ved hjelp av det vi har funnet ut, og sammenlikn med det du får om du prøver å tegne den på kalkulator.