Fra en funksjon til en graf
Hva er en graf? Hvordan finner vi grafen til en funksjon?
Vi har sett at en funksjon kan representeres med en regneregel, for eksempel kan funksjonen "gang med 4" skrives som . En annen måte å representere en funksjon på er ved å tegne en graf. Ved hjelp av funksjonsuttrykket kan vi for enhver verdi av regne ut funksjonsverdien, som vi kaller . Hvis vi sammenholder en slik med sin tilhørende får vi et tallpar , og dette kan vi tenke på som et punkt i et koordinatsystem. Ved å tegne streker mellom slike punkt får vi en kurve som vi kaller funksjonens graf. Her skal vi vise noen eksempler.
Eksempel 1
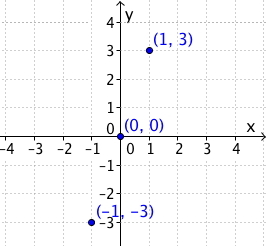
Tegn grafen til funksjonen .
For å tegne grafen til en funksjon, må vi først finne noen punkter som ligger på grafen. Vi begynner med å lage en tabell med to rader: Én rad for x-verdier (som vi velger fritt) og én rad for de tilhørende y-verdiene. I dette eksempelet velger vi x-verdiene , og .
Vi setter inn en og en verdi for i funksjonsuttrykket og regner ut en og en -verdi. For eksempel setter vi inn i , og får at . På samme måte finner vi de to andre y-verdiene, og da kan vi fylle ut tabellen:
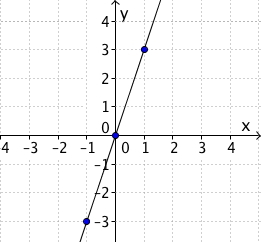
For hver i tabellen har vi en tilhørende -verdi. Disse danner tallpar . Hvert tallpar er et punkt i koordinatsystemet, og nå har vi det vi trenger for å tegne grafen. Vi markerer de tre punktene i et koordinatsystem (-aksen er vannrett og -aksen er loddrett), og så tegner vi en linje som går gjennom alle tre punkter.
Grafen er en rett linje, og dette kan man faktisk vite bare ved å se på funksjonen. Variabelen er i første potens, og da er grafen en rett linje. Dette trenger vi ikke vite for å tegne grafen, men det hjelper å vite slikt for å sjekke resultatet.
Siden grafen er en rett linje kunne vi egentlig tegnet den bare ved hjelp av to punkter, men det er bedre å velge tre eller flere for å gjøre det lettere å oppdage om vi har gjort noen regnefeil.
Eksempel 2
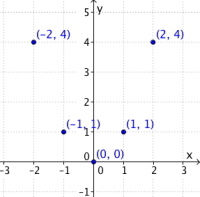
Tegn grafen til funksjonen .
Som i det forrige eksempelet begynner vi med å tegne en tabell. Om vi prøver med tre punkter som over ser vi at det er litt vanskelig å vite hvordan grafen ser ut, så vi velger oss fem forskjellige x-verdier å regne ut tilhørende y-verdier for. For eksempel gir at
.
Tabellen vår blir da seende slik ut:
Nå har vi fem punkter som ligger på grafen til funksjonen vår, og tegner inn punktene i et koordinatsystem.
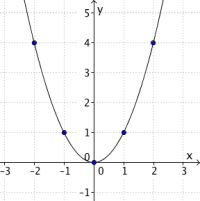
Hvis du nå prøver å tegne en rett linje, ser du at det ikke går. Grafen til funksjonen må gå gjennom alle punktene vi har regnet ut, og derfor har denne funksjonen en graf som ser slik ut:
Igjen kunne vi sett på funksjonen at grafen måtte ha denne formen - variabelen er i andre potens, og andregradsfunksjoner har buet form som den over.
Del på Facebook
Lynkurs, 8.-10.trinn
Funksjoner (del I)
Består av:
- Hva er en funksjon?
- Koordinatsystem
- Fra en funksjon til en graf
- Rette linjer (lineære funksjoner)
- Proporsjonalitet
- Fra en graf til en funksjon
- Andregradsfunksjoner
- Funksjonsgrafer for andregradsfunksjoner
- Hvorfor ser grafen ut som den gjør?
- Inger Christin forteller om funksjoner.
- Test deg selv i lineære funksjoner!
- Test deg selv i funksjoner!
Begrep
-
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
-
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
-
Koordinatsystem
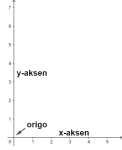
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
-
Verditabell
En tabell med verdier av en variabel, for eksempel , og tilhørende funksjonsverdier, for eksempel , kalles for en verditabell.
Verditabellen gir oss oversikt over verdier som hører sammen. Den hjelper oss enten med å finne punkter som ligger på grafen til en funksjon eller funksjonsuttrykket til en graf.
-
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse. -
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.