Kritiske punkter

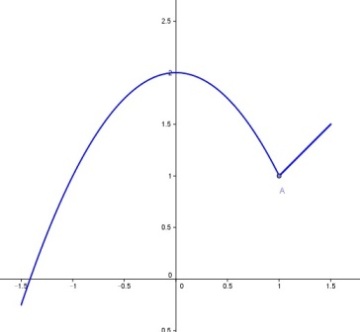
Et eksempel på en graf der det kritiske punktet A er et lokalt minimum, mens endepunktet er et globalt minimum.

Når vi leter etter topp- og bunnpunkter, ser vi først etter punkter der den deriverte er null. Vi vet at hvis funksjonen $f\left(x\right)$ er sammenhengende (kontinuerlig) og deriverbar, så er nemlig nullpunktene til den deriverte lokale topp- eller bunnpunkter. Det er imidlertid også andre kandidater som kan være topp- eller bunnpunkter. I figuren til høyre ser vi for eksempel at endepunktene kan være bunnpunkter. Det samme gjelder punkter hvor funksjonen $f\left(x\right)$ ikke er deriverbar, for eksempel der den har en «knekk».

For å få litt orden på dette, lager vi en ny definisjon:

Grunnen til at vi tar oss bryet med å gi en samlebetegnelse på disse punktene, er følgende teorem.

Hva er det som er så fint med dette? Jo, hvis du ser nøye på definisjonen av de kritiske punktene, ser du at det er nøyaktig de samme punktene som skal avmerkes på fortegnslinja til $f\prime \left(x\right)$. Teoremet over garanterer dermed at hvis du lager fortegnslinja til $f\prime \left(x\right)$, så vil alle ekstremalpunktene til $f$ være blant punktene du har merket av. Vi skal se på et eksempel.

Eksempel

Vi ser på en funksjon definert med delt forskrift, og vi ønsker å finne alle topp- og bunnpunkter, samt avgjøre hvilke som er globale.

$f\left(x\right)=\left\{\begin{array}{cc}{x}^2& -2\le x\le 1\\ 2-x& 1<x\le 3\end{array}\right.$

Her er definisjonsområdet $\left[-2,3\right]$. Vi må regne ut den deriverte av $f$:

$f\text{'}\left(x\right)=\left\{\begin{array}{cc}2x& -2\le x<1\\ -1& 1<x\le 3\end{array}\right.$

Merk at $f$ ikke er deriverbar i $x=1$ (se punkt 2 under). Vi går gjennom og finner de tre typene kritiske punkter.

1. Punkter der $f\text{'}\left(x\right)=0$. Det eneste slike punktet er $x=0$.

2. Punkter der $f$ ikke er deriverbar. Fra lynkurset om deriverbarhet vet vi at $f$ er deriverbar i et punkt $a$ hvis $f$ er kontinuerlig i $a$ og $\underset{x\to a^{-}}{\lim }f\text{'}\left(x\right)=\underset{x\to a^{+}}{\lim }f\text{'}\left(x\right)$. $f$ er kontinuerlig i $x=1$, men det andre kravet gjelder ikke (sjekk selv!). Dermed finnes ikke den deriverte her.

3. Endepunktene. Dette er $x=-2$ og $x=3$.

Hvis vi tegner fortegnslinja til $f\text{'}$ ser det slik ut:

Alle de kritiske punktene kan sees på fortegnslinja. Vi kan også si hva slags type punkt de er: $x=-2$ er et toppunkt siden funksjonen minker mot høyre, mens $x=3$ er et bunnpunkt fordi funksjonen stiger mot venstre. I $x=0$ er den deriverte 0 og skifter fortegn fra negativt til positivt, så dette er et bunnpunkt. I $x=1$ er ikke den deriverte definert, men funksjonen er kontinuerlig her, og den deriverte skifter fra positivt til negativt fortegn, så dette er et toppunkt.

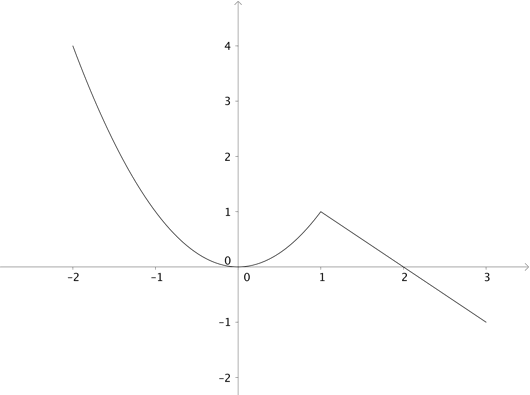
Alt dette kan vi også se på grafen til funksjonen:

Av bildet ser vi at endepunktene er globalt maksimum og minimum, henholdsvis. Det kan vi også regne ut direkte:

• Toppunktene er $x=-2$ og $x=1$. $f\left(-2\right)=4$, mens $f\left(1\right)=1$. Dermed er $x=-2$ et globalt toppunkt.
• Bunnpunktene er $x=0$ og $x=3$. $f\left(0\right)=0$, mens $f\left(3\right)=-1$. Dermed er $x=3$ et globalt bunnpunkt.

Til slutt en advarsel: Hvis ikke funksjonen var kontinuerlig i $x=1$ (da sier vi at dette er et bruddpunkt) kunne vi ikke vært sikre på at det var et toppunkt. Prøv for eksempel å bytte ut $2-x$ med $x-1$ i definisjonen av $f$ og tegne det du får. Du vil se at $x=1$ fortsatt er et toppunkt, men den deriverte skifter ikke fortegn. I bruddpunkt kan det meste skje!