Fortegnslinja 3 - funksjoner bestående av flere faktorer

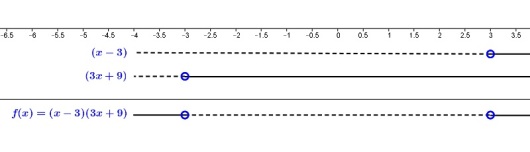
La oss tegne fortegnslinja til funksjonen $f\left(x\right)=\left(x-3\right)\left(3x+9\right)$. Først tegner vi fortegnslinja til hver av faktorene $\left(x-3\right)$ og $\left(3x+9\right)$, og så setter vi disse sammen til fortegnslinja til hele funksjonen.

Til dette bruker vi fortegnsreglene for multiplikasjon/divisjon:

            $\left(+\right)\cdot \left(+\right)=\left(+\right)$              $\left(+\right)\cdot \left(-\right)=\left(-\right)$

            $\left(-\right)\cdot \left(-\right)=\left(+\right)$              $\left(-\right)\cdot \left(+\right)=\left(-\right)$

Vi begynner med å finne nullpunktet til $\left(x-3\right)$:

$\left(x-3\right)=0$

$x=3$

$\left(x-3\right)$ har $x=3$ som eneste nullpunkt. Vi ser også at $\left(x-3\right)$ er positiv når $x$ er større enn $3$ $\left(x>3\right)$ og negativ når $x$ er mindre enn $3$ ($x<3$).

Vi finner nå nullpunktet til $\left(3x+9\right)$:

 $\left(3x+9\right)=0$

$3x=-9$

$x=-3$

$\left(3x+9\right)$ har $x=-3$ som eneste nullpunkt. Vi ser også at $\left(3x+9\right)$ er positiv når $x$ er større enn $-3$ ($x>-3$) og negativ når $x$ er mindre enn $-3$ ($x<-3$).

Vi kan nå finne tallinja til $f\left(x\right)$. Siden $\left(x-3\right)$ og $\left(3x+9\right)$ er faktorer i $f\left(x\right)$, er deres nullpunkter også nullpunkter i funksjonen, så vi tegner inn de samme nullpunktene. Så bruker vi fortegnsreglene for multiplikasjon/divisjon til å finne fortegnet mellom nullpunktene:

Begge linjene viser negativ verdi                    $\Rightarrow$        funksjonen får positiv verdi

En linje viser positiv, den andre negativ          $\Rightarrow$        funksjonen får negativ verdi

Begge linjene viser positiv                              $\Rightarrow$        funksjonen får positiv verdi

Eksempel 1

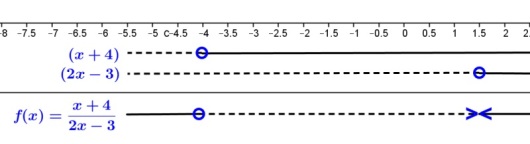
Oppgave. Finn fortegnslinja til

$f\left(x\right)=\frac{x+4}{2x-3}$.

Løsning. Vi ser på teller og nevner for seg og lager fortegnslinja til $f\left(x\right)$ ved å sette de to sammen.

$\left(x+4\right)$ har nullpunkt $x=-4$ og er positiv for $x$ større enn $-4$ ($x>-4$) og negativ for $x$ mindre enn $-4$ ($x<-4$).

$\left(3-2x\right)$ har nullpunkt $x=\frac{3}{2}$ og er positiv for $x$ mindre $\frac{3}{2}$ ($x<\frac{3}{2}$) og negativ for $x$ større enn $\frac{3}{2}$ ($x>\frac{3}{2}$).

Husk: Når nevneren er 0, er funksjonen mest sannsynlig ikke definert. Det eneste tilfellet der funksjonen fremdeles er definert når nevneren er null, er hvis telleren også er null.

I vårt tilfelle er ikke telleren $0$, og $f\left(x\right)$ er ikke definert i nullpunktet til nevneren $\left(2x-3\right)$. Bortsett fra dette gjør vi det samme som før:

Eksempel 2

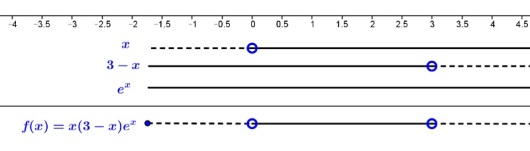
Oppgave. Lag fortegnslinja til $f\left(x\right)=x\left(3-x\right)e^x$.

Løsning. Funksjonsuttrykket til $f\left(x\right)$ er lik produktet av faktorene

$x$, $\left(3-x\right)$ og $e^x$.

$x$ har nullpunkt i $x=0$, $\left(3-x\right)$ i $x=3$, mens $e^x$ alltid er positiv. Vi lager en fortegnslinje for hver av dem, og tegner dem i samme skjema (se figuren under). Til slutt tegner vi fortegnslinja til $f\left(x\right)$ nederst ved å bruke fortegnsreglene. For eksempel blir $f\left(x\right)$ negativ på intervallet $\left(-\infty ,0\right)$, fordi der er $x$ negativ, mens de to andre faktorene er positive.