Derivasjon av vektorfunksjoner 3

Vi har en 

$\overrightarrow{r\left(t\right)}=\left[x\left(t\right),y\left(t\right)\right]=\left[2t,-\frac{3}{5}{t}^2+6t\right]$          

som beskriver posisjonen til en ball som blir kastet bortover en slette. $t$ er tiden. Vi er interessert i å finne farten til ballen.

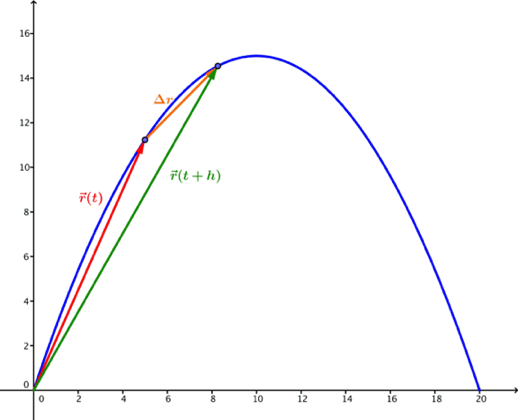
Vi begynner med å finne gjennomsnittlig fart i en periode. Vi vil finne gjennomsnittlig fart mellom en tid $t$ og $t+h$.

Vi definerer

$\Delta \overrightarrow{r}=\overrightarrow{r}\left(t+h\right)-\overrightarrow{r}\left(t\right)$.

Eksempel

Hvis vi har $t=1$ og $h=1$ får vi

$\Delta \overrightarrow{r}=\overrightarrow{r}\left(2\right)-\overrightarrow{r}\left(1\right)=\left[2\cdot 2,-\frac{3}{5}\cdot 2^2+6\cdot 2\right]-\left[2\cdot 1,-\frac{3}{5}\cdot 1^2+6\cdot 1\right]$           

$=\left[4,\frac{48}{5}\right]-\left[2,\frac{27}{5}\right]=\left[2,\frac{21}{5}\right]$.

$\Delta \overrightarrow{r}$ er endringen i posisjon i løpet av $h$ sekunder etter tidspunktet $t$. For å finne gjennomsnittlig endring, deler vi simpelthen på $h$:

$\overrightarrow{v_h}=\frac{\Delta \overrightarrow{r}}{h}=\frac{\left[2,\frac{21}{5}\right]}{1}=\left[2,\frac{21}{5}\right]$.

La nå $h$ gå mot null og finn gjennomsnittlig fart i et mindre og mindre tidsrom. Når vi lar $h$ gå mot null, går $\Delta \overrightarrow{r}$ mot å tangere kurven i punktet $t$. $\overrightarrow{v_h}$ er $\Delta \overrightarrow{r}$ delt på en konstant, og har derfor samme retning som $\Delta \overrightarrow{r}$, så også $\overrightarrow{v_h}$ går mot å tangere kurven.

La oss se hva som skjer med $\overrightarrow{v_h}$ når $h$ går mot null. Husk at $\overrightarrow{r}\left(t\right)=\left[x\left(t\right),y\left(t\right)\right]$.

 $\overrightarrow{v}\left(t\right)=\underset{h\to 0}{\lim }\frac{\Delta r}{h}$            

$=\underset{h\to 0}{\lim }\frac{\overrightarrow{r}\left(t+h\right)-\overrightarrow{r}\left(t\right)}{h}$ 

$=\underset{h\to 0}{\lim }\frac{\left[x\left(t+h\right),y\left(t+h\right)\right]-\left[x\left(t\right),y\left(t\right)\right]}{h}$

$=\underset{h\to 0}{\lim }\left[\frac{x\left(t+h\right)-x\left(t\right)}{h},\frac{y\left(t+h\right)-y\left(t\right)}{h}\right]$

$=\left[\underset{h\to 0}{\lim }\frac{x\left(t+h\right)-x\left(t\right)}{h},\underset{h\to 0}{\lim }\frac{y\left(t+h\right)-y\left(t\right)}{h}\right]$

$=\left[x\text{'}\left(t\right),y\text{'}\left(t\right)\right]$.

Vi ser altså at vi ender opp med en fartsvektor $\overrightarrow{v}\left(t\right)=\left[x\text{'}\left(t\right),y\text{'}\left(t\right)\right]$ som er retningsvektor for tangenten til grafen i $t$. Den angir da både retningen ballen beveger seg i og hvor fort det går i $t$. Dette er den deriverte av vektorfunksjonen.

Eksempel på bruk av definisjonen

Vi ser på det samme eksempelet med en ball som blir kastet:

            $\overrightarrow{r}\left(t\right)=\left[2t,-\frac{3}{5}{t}^2+6t\right]$

Da har vi:

            $\overrightarrow{r}\text{'}\left(t\right)=\left[x\text{'}\left(t\right),y\text{'}\left(t\right)\right]=\left[2,-\frac{6}{5}t+6\right]$

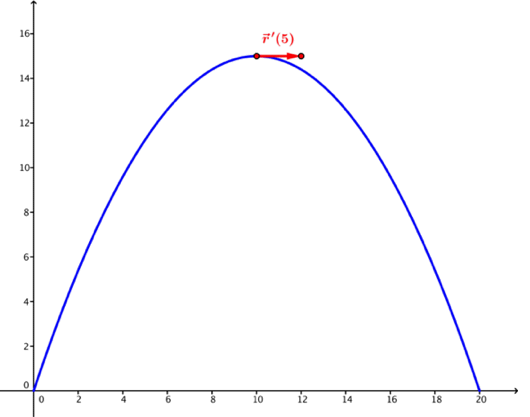
La oss se på den deriverte i $t=5$:

            $\overrightarrow{r}\text{'}\left(5\right)=\left[2,-\frac{6}{5}\cdot 5+6\right]=\left[2,0\right]$

Da er ballen i punktet $\overrightarrow{r}\left(5\right)=\left[10,15\right]$.

Legg merke til at ballen i dette punktet bare beveger seg i $x$-retning, den har altså sluttet å bevege seg oppover og har enda ikke begynt å bevege seg nedover. Dette er altså toppunktet.