Definisjon av den deriverte

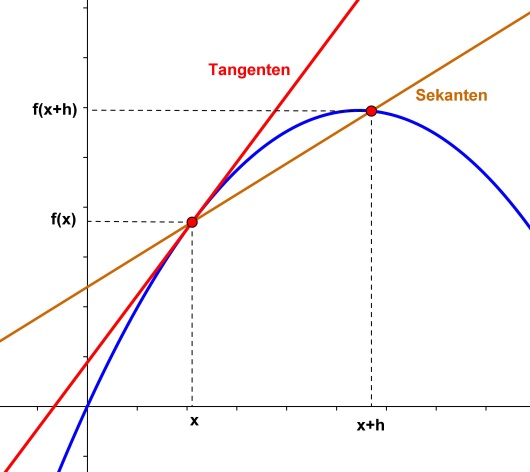
Vi har kommet fram til at momentan vekstfart til en funksjon $f (x)$ i $a$ , er stigningstallet til tangenten til funksjonen i $a$ . Tangenten kan finnes grafisk eller med lommeregner, men dette er jo håpløst unøyaktig! Som gode matematikere vil vi helst ha en matematisk metode for å finne dette stigningstallet.

Vi er ønsker å finne en metode for å regne ut momentan vekstfart for $f (x)$ i et punkt $x$ . Vi starter med to punkter $x$ og $(x + h)$ på x-aksen og tegner

Sekant

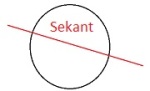
En linje som skjærer en kurve. En korde er en del av en sekant. En sekant er ikke det samme som en tangent.

sekanten

mellom

(x, f (x))

(x + h, f (x + h))

, det vil si at vi tegner den rette linja som skjærer funksjonen i disse to punktene (vist på figuren under).

Stigningstall

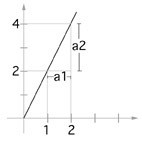
Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

Stigningstallet

til denne sekanten er det vi tidligere omtalte som

Gjennomsnittlig vekstfart

En funksjon $f (x)$ har gjennomsnittlig vekstfart

$\frac{Δ y}{Δ x} = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$

mellom $x_{2}$ og $x_{1}$ . Dette er gjennomsnittlig økning i y-retning per økning i x-retning på intervallet.

gjennomsnittlig vekstfart

mellom

x

x + h

\frac{Δ y}{Δ x} = \frac{f (x + h) - f (x)}{h}

Hvis vi lar $h$ bli mindre og mindre, så nærmer sekanten seg mer og mer tangenten, fordi punktet $(x + h, f (x + h))$ kommer nærmere og nærmere $(x, f (x))$ .

Stigningstallet til tangenten blir grenseverdien til stigningen til sekanten når $h$ går mot null:

\lim_{h \to 0} \frac{f (x + h) - f (x)}{h}

Hvis denne grensen eksisterer kaller vi den den deriverte av $f$ i $x$ .

Definisjon

Den deriverte til $f$ i $x$ er $f' (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h}$ .

Det er mange notasjoner for den deriverte (kjært barn har mange navn!). Hvis $f (x) = x^{2} + 3 x$ , kan skrive den deriverte som

f' (x), \overset{\cdot}{f}, [x^{2} + 3 x]', \frac{d f}{d x}

Eksempel 1

Oppgave. Finn den deriverte av funksjonen $f (x) = x^{2}$ .

Løsning.

f' (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h} = \lim_{h \to 0} \frac{{(x + h)}^{2} - x^{2}}{h} = \lim_{h \to 0} \frac{x^{2} + 2 x h + h^{2} - x^{2}}{h}

= \lim_{h \to 0} \frac{2 x h + h^{2}}{h} = \lim_{h \to 0} \frac{2 x h}{h} + \frac{h^{2}}{h} = \lim_{h \to 0} 2 x + h = 2 x

Eksempel 2

Oppgave. Finn den deriverte av funksjonen $f (x) = \frac{1}{x}$ .

Løsning.

f' (x) = \lim_{h \to 0} \frac{f (x + h) - f (x)}{h} = \lim_{h \to 0} \frac{\frac{1}{x + h} - \frac{1}{x}}{h} = \lim_{h \to 0} \frac{\frac{x}{x (x + h)} - \frac{x + h}{x (x + h)}}{h}

= \lim_{h \to 0} \frac{x - x - h}{h x (x + h)} = \lim_{h \to 0} \frac{- h}{h x (x + h)} = \lim_{h \to 0} \frac{- 1}{x (x + h)} = - \frac{1}{x^{2}}

Geometrisk eksempel

Den deriverte er selv en funksjon, som vi har sett: Man tegner linja som i hvert punkt består av grenseverdien i definisjonen over. I de to GeoGebra-arkene under kan du prøve dette selv, og se på to forskjellige funksjoner hvordan den deriverte er bygget opp. Hvis du flytter punktet A langs funksjonen vil du se at punktet B, som angir den deriverte, flytter seg. Om du så høyreklikker på B og velger "trace on" vil du kunne flytte A fram og tilbake og få fram den deriverte til funksjonen.

Derivasjon 1

Derivasjon 2

Del på Facebook

Del på Facebook