Introduksjon til derivasjon – gjennomsnittlig og momentan vekstfart
Du skal ut på fjelltur og lurer på omtrent hvor langt du kommer på en dag. Dette avhenger av hvor langt du går, men også hvor bratt stigningen på turen er. Stigningen er et mål på hvor fort det går oppover, altså hvor mye du går oppover for hver meter du beveger deg i vannrett retning.
Du velger deg to steder på fjellet – et start- og et stoppunkt. Vi antar for enkelhets skyld at du går rett opp, altså at stien ikke svinger. Du finner ut hvor langt det er mellom start og stopp i vannrett retning (langs x-aksen) og hvor langt det er mellom de to i loddrett retning (langs y-aksen). Vi kaller disse avstandene for Δx og Δy. Nå blir stigningen forholdet mellom Δy og Δx, ΔyΔx, altså, hvor mye går vi oppover for hver enhet vi går bortover.
Gjennomsnittlig vekstfart og momentan vekstfart:
Hvis vi nå tenker oss at høyden til fjellet er bestemt av x ved en funksjon f(x), kan vi lage en definisjon for den gjennomsnittlige vekstfarten. Det er farten funksjonen ville steget i dersom den steg like raskt hele veien.
Definisjon. Gjennomsnittlig vekstfart
Den gjennomsnittlige vekstfarten til en funksjon f(x) mellom to punkter på x-aksen, x1 og x2, er
ΔyΔx=f(x2)-f(x1)x2-x1.
Hvis vi flytter de to punktene nærmere og nærmere hverandre, kan vi tenke oss at vi kommer nærmere og nærmere en slags stigningsfart i ett punkt. Gir det mening? Kan vi finne vekstfarten til en funksjon, ikke på et intervall, men rett og slett i et punkt? Svaret er ja, og dette kaller vi momentan vekstfart. Ta eksempelet med fjellet igjen. Hva ville skjedd hvis fjellet fortsatte å ha samme vekstfart, ha den samme stigningen, som i et punkt a videre? Da ville funksjonen sett ut som en lineær funksjon t(x) som går gjennom punktet (a,f(a)) og har samme stigning som f har i punktet a.
Stigningstall
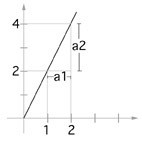
Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.
Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.
Definisjon. Momentan vekstfart
Den momentane vekstfarten til funksjonen f(x) når x=a er stigningstallet til
Tangent
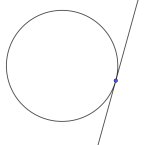
Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.
Del på Facebook
Lynkurs 11.-13.trinn
Derivasjon
Består av:
- Introduksjon til derivasjon – gjennomsnittlig og momentan vekstfart
- Definisjon av den deriverte
- Deriverbarhet
- Derivasjonsregler
- Kjerneregelen
- Kjerneregelen - tre eksempler
- Derivasjon av sammensatte uttrykk
- Å finne tangenten - introduksjon
- Ettpunktsformelen og likning for tangentlinjen
- Høyere ordens deriverte
- Derivasjon av vektorfunksjoner 1 - Parameterframstilling
- Derivasjon av vektorfunksjoner 2 - vektorfunksjoner
- Derivasjon av vektorfunksjoner 3





