Grenseverdisetningene

Vi starter med et teorem, som vi så bruker på noen eksempler.

La oss for eksempel ta grenseverdien $\underset{x\to 2}{\lim }(x^2+\text{ln }x)\mathrm{.}$ 

Vi bruker grenseverdisetning 1: Dersom grenseverdiene eksisterer, har vi at

$\underset{x\to 2}{\lim }(x^2+\text{ln }x)=\underset{x\to 2}{\lim }{x}^2+\underset{x\to 2}{\lim }\text{ln }x\mathrm{.}$

Fordi både $x^2$ og $\text{ln} x$ er kontinuerlige i sine definisjonsområder, og derfor spesielt i $x=2$, får vi dermed at

 $\underset{x\to 2}{\lim }(x^2+\text{ln }x)=\underset{x\to 2}{\lim }{x}^2+\underset{x\to 2}{\lim }\text{ln }x=2^2+\text{ln }2=4+\text{ln }2.$

Det er nesten alltid lett å beregne grenseverdier på formen $\underset{x\to a}{\lim }f\left(x\right)$ når $f\left(x\right)$ er definert i $x=a\mathrm{.}$ Så lenge $f$ er kontinuerlig, 
er det bare å sette inn $x=a$ i uttrykket og regne ut. Problemene kommer dersom $f\left(x\right)$ ikke er definert når $x=a$. Et typisk eksempel på dette er når uttrykket til $f\left(x\right)$ er en brøk,

$f\left(x\right)=\frac{g\left(x\right)}{h\left(x\right)},$

der $h\left(a\right)=0$. I slike situasjoner er det to muligheter. Dersom $g\left(a\right)$ er forskjellig fra 0, er saken grei. Da eksisterer ikke grenseverdien, fordi

 $\underset{x\to a}{\lim }f\left(x\right)=\underset{x\to a}{\lim }\frac{g\left(x\right)}{h\left(x\right)}="\frac{g\left(a\right)}{0}"=\pm \infty$.

Hvis $g\left(a\right)=0$, sier vi gjerne at vi har et "$\frac{0}{0}$"-uttrykk. I slike tilfeller kan det hende at grenseverdien eksisterer, men vi må ofte bruke noen triks for å finne den. Det mest grunnleggende trikset, som vi viser i de neste to eksemplene, er å forkorte brøken.

Eksempel 1

Oppgave. Finn grenseverdien $\underset{x\to 2}{\lim }\frac{2x^2-4x}{x-2}$ hvis den eksisterer.

Løsning. Her blir både teller og nevner lik null dersom vi setter inn $x=2$. I slike tilfeller kan vi finne grenseverdien ved å forkorte brøken. Vi finner:

 $\underset{x\to 2}{\lim }\frac{2x^2-4x}{x-2}=\underset{x\to 2}{\lim }\frac{2x(x-2)}{x-2}=\underset{x\to 2}{\lim }2x=4$.

Eksempel 2

Oppgave. Finn grenseverdien $\underset{x\to 3}{\lim }\frac{3-x}{2-\sqrt{x+1}}$ hvis den eksisterer.

Løsning. Både teller og nevner blir lik null når $x=3$, så vi kan ikke sette inn direkte. Som i forrige eksempel ønsker vi å forkorte brøken, men for å få til det, må vi ordne litt på uttrykket. Ifølge 

Konjugatsetningen

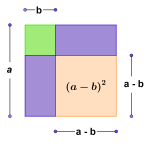
Konjugatsetningen kalles også tredje kvadratsetning:

 $(a+b)(a-b)=a^2-b^2$.

konjugatsetningen

 $(2-\sqrt{x+1})(2+\sqrt{x+1})=4-(x+1)=3-x\mathrm{.}$

Dersom vi ganger oppe og nede i brøken med $2+\sqrt{x+1}$, får vi derfor

 $\frac{3-x}{2-\sqrt{x+1}}=\frac{(3-x)\cdot (2+\sqrt{x+1})}{(2-\sqrt{x+1})\cdot (2+\sqrt{x+1})}=\frac{(3-x)(2+\sqrt{x+1})}{3-x}=2+\sqrt{x+1}\mathrm{.}$

Dermed fikk vi forkortet bort hele nevneren, og grenseverdien er

 $\underset{x\to 3}{\lim }\frac{3-x}{2-\sqrt{x+1}}=\underset{x\to 3}{\lim }(2+\sqrt{x+1})=2+\sqrt{3+1}=4.$