Kontinuitet
Kontinuitet er et av de viktigste begrepene i matematikken. En kontinuerlig funksjon er, enkelt sagt, en funksjon som "henger sammen" når man tegner grafen - du kan tegne den uten å løfte hånda fra papiret.
Som matematikere må vi ha en mer presis definisjon enn at man ikke trenger å løfte hånda fra papiret når man tegner. Vi trenger noe vi kan bruke på en funksjon som er oppgitt ved hjelp av formler – det er ikke alle funksjoner vi kan tegne for å teste kontinuitet. Nå som vi vet hva en grenseverdi er kan vi definere kontinuitet skikkelig:
|
Definisjon. Kontinuitet Hvis er definert for , sier vi at er kontinuerlig i punktet dersom . Dersom er kontinuerlig i alle punktene i et intervall, sier vi at er kontinuerlig i intervallet. |
Definisjonen over er kanskje litt vanskelig å lese hvis man ikke er vant til grenseverdier. En mindre formell måte å tenke på det på er at når nærmer seg , nærmer funksjonsverdien i seg funksjonsverdien i . Det vil si at når du beveger deg langs -aksen kommer det ikke noen plutselige "hopp" i funksjonen, altså henger linja du tegner sammen.
En del funksjoner er kontinuerlige overalt – for eksempel er det. Da sier vi ofte bare at er kontinuerlig. Man kan vise at de aller fleste "standardfunksjonene" vi jobber med er kontinuerlige i sine definisjonsområder. Dette gjelder for eksempel
- potensfunksjoner, som og ,
- eksponential- og logaritmefunksjoner, som og ,
- de trigonometriske funksjonene sin , cos og tan .
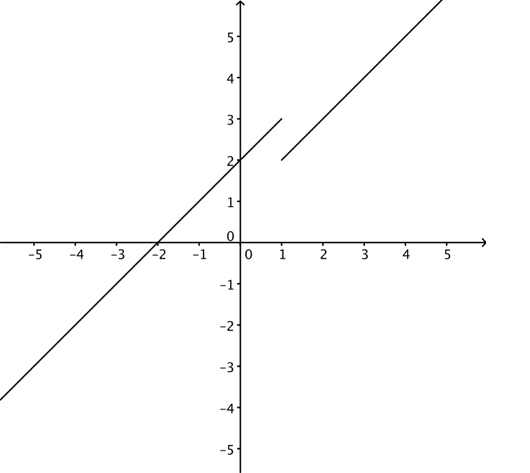
Under har vi tegnet en funksjon som ikke er kontinuerlig:
Del på Facebook