Asymptoter

Nå som vi har lært oss å regne med grenseverdier kan vi snakke om en annen viktig idé: Asymptoter. En asymptote er en linje som en funksjon kommer stadig nærmere, men ikke møter.

Definisjon. Asymptoter

La $c$ være et tall.

Dersom $\lim_{x \to + \infty} f (x) = c$ og/eller $\lim_{x \to - \infty} f (x) = c$ , sier vi at $y = c$ er en horisontal asymptote for $f$ .
Dersom $\lim_{x \to c^{-}} f (x) = \pm \infty$ og/eller $\lim_{x \to c^{+}} f (x) = \pm \infty$ , sier vi at $x = c$ er en vertikal asymptote for $f$ .

Vi gikk rett på med en definisjon, men om man synes det blir mye symboler kan man si det mindre formelt:

Dersom $f (x)$ går mot et fast tall når $x$ går mot uendelig, har grafen en horisontal asymptote.

Dersom $f (x)$ går mot uendelig når $x$ går mot et fast tall, har grafen en vertikal asymptote.

Definisjonen er fin å ha med å gjøre, i den forstand at den kan brukes direkte når vi skal finne asymptoter. Teknikken er som følger:

Regel. Å finne asymptoter

Horisontale asymptoter: Regn ut $\lim_{x \to + \infty} f (x)$ og $\lim_{x \to - \infty} f (x)$ . Dersom noen av disse eksisterer, bruk definisjon 1.
Vertikale asymptoter: Identifisér alle bruddpunkter og punkter der $f (x)$ ikke er definert, og undersøk grenseverdiene i hvert tilfelle. Dersom noen av disse blir $+ \infty$ eller $- \infty$ , bruk Definisjon 2.

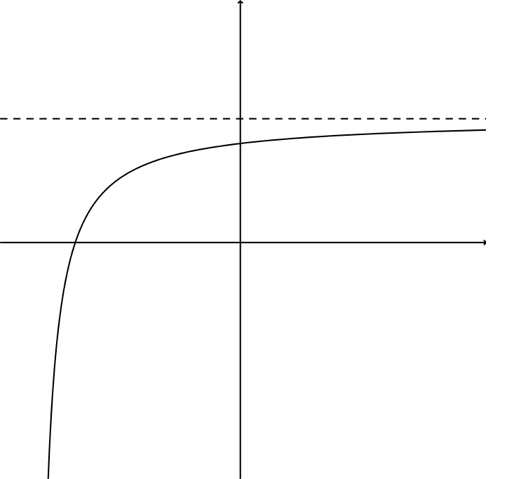
En graf med en horisontal asymptote.

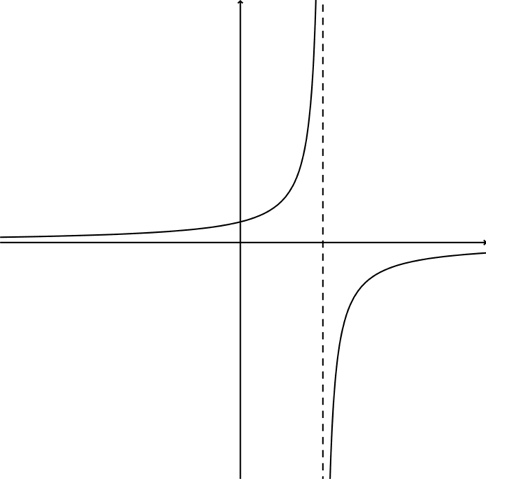
En graf med en vertikal asymptote

Eksempel

Oppgave. Finn alle horisontale og vertikale asymptoter til $f (x) = \frac{1}{x}$ .

Løsning. Som vi allerede har sett, er $\lim_{x \to \pm \infty} \frac{1}{x} = 0$ . Dette viser at $y = 0$ er en horisontal asymptote for $f$ .

Den eneste muligheten for vertikal asymptote er $x = 0$ . ( $f$ har ingen bruddpunkter, og er kontinuerlig overalt utenom i $x = 0$ .)

Fordi

$\lim_{x \to 0 -} \frac{1}{x} = - \infty$ og $\lim_{x \to 0 +} \frac{1}{x} = + \infty$

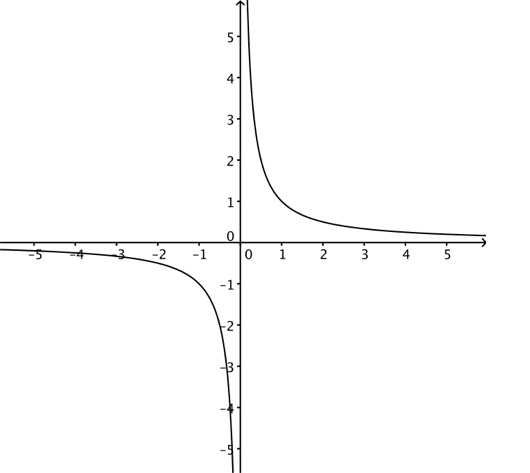
konkluderer vi med at $x = 0$ er en vertikal asymptote for $f$ . Sammenlign med grafen på figuren nedenfor.

Asymptoter

Eksempel

Lynkurs 11.-13.trinn

Grenseverdier og asymptoter

Består av: