Ensidige grenseverdier

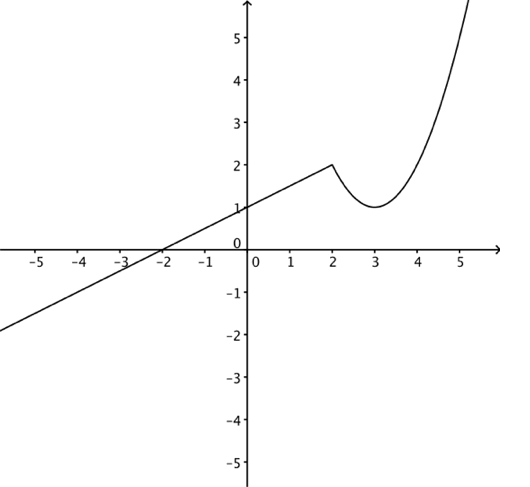
Se på følgende funksjon:

 $f\left(x\right)=\{\begin{array}{cc}1+\frac{1}{2}x& x<2\\ x^2-6x+10& x\ge 2\end{array}$
Her støter vi på problemer hvis vi skal regne ut $\underset{x\to 2}{\lim } f\left(x\right)$, fordi funksjonsuttrykket er avhengig av hvilken side av 2 vi er på.

Hva kan vi bruke denne definisjonen til? Dette teoremet er et eksempel:

Eksempel 1

Oppgave. La funksjonen $f$ være gitt ved

 $f\left(x\right)=\{\begin{array}{cc}1+\frac{1}{2}x& x<2\\ x^2-6x+10& x\ge 2\end{array}$ 

Undersøk om $f$ er kontinuerlig i $x=2$.

Løsning. Vi regner ut at

 $\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }\left(1+\frac{1}{2}x\right)=2$

og

 $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(x^2-6x+10\right)=2^2-6\cdot 2+10=2=f\left(2\right)$.

Her brukte vi at polynomfunksjoner er kontinuerlige, så vi kunne sette inn $x=2$ direkte. Siden de tre verdiene ble like, kan vi konkludere med at funksjonen er kontinuerlig i bruddpunktet – og dermed overalt. Grafen til $f$ har en knekk i punktet $x=2$, men du kan fremdeles tegne den uten å løfte blyanten fra papiret.

Eksempel 2

Oppgave. Undersøk om funksjonen

$g\left(x\right)=\{\begin{array}{cc}-1& x<0\\ 1& x\ge 0\end{array}$  er kontinuerlig i bruddpunktet $x=0$.

Løsning. Her blir de ensidige grenseverdiene

$\underset{x\to 0-}{\lim }g\left(x\right)=\underset{x\to 0-}{\lim }(-1)=-1$, mens $\underset{x\to 0+}{\lim }g\left(x\right)=\underset{x\to 0+}{\lim }1=1$.

Disse er ikke like, så funksjonen er ikke kontinuerlig. Det er en god idé å tegne grafen til $g$ selv, og sjekke at du får samme konklusjon ut fra den.