Asymptoter - et eksempel

Oppgave. Finn alle horisontale og vertikale asymptoter til

 $f\left(x\right)=\{\begin{array}{cc}{e}^{2x-1}+\frac{1}{2}& x<1\\ \frac{3-2x}{x-1}& x>1\end{array}$ 

Løsning.


Horisontale asymptoter: Vi finner grensene $\underset{x\to -\infty }{\lim }f\left(x\right)$ og $\underset{x\to +\infty }{\lim }f\left(x\right)$. Når $x$ er negativ, er det $f\left(x\right)=e^{2x-1}+\frac{1}{2}$ som gjelder, slik at

$\underset{x\to -\infty }{\lim }f\left(x\right)=\underset{x\to -\infty }{\lim }(e^{2x-1}+\frac{1}{2})=0+\frac{1}{2}=\frac{1}{2}$.

(Her brukte vi at når $x\to -\infty$, så vil også $2x-1\to -\infty$. Uttrykket $e^{2x-1}$ går da
mot 0.) Dette viser at $y=1$ er horisontal asymptote for $f$.

Når $x$ er større enn $1$, er $f\left(x\right)=\frac{3-2x}{x-1}$. Ved å dividere med $x$ oppe og nede, finner vi at

$\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{3-2x}{x-1}=\underset{x\to +\infty }{\lim }\frac{\frac{3}{x}-2}{1-\frac{1}{x}}=\frac{0-2}{1-0}=-2$.

Dette gir en ny horisontal asymptote, nemlig $y=-2$.

Vertikale asymptoter: Disse kan forekomme i bruddpunkter og i punkter der funksjonen ikke er definert. I vårt tilfelle ser vi at $x=1$ er den eneste muligheten. Fordi dette er et bruddpunkt, må vi bruke ensidige grenseverdier for å undersøke hva som skjer når $x$ nærmer seg $1$:

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }(e^{2x-1}+\frac{1}{2})=e^{2\cdot 1-1}+\frac{1}{2}=e+\frac{1}{2}$,

$\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\frac{3-2x}{x-1}="\frac{1}{0}"$ .

Når $x\to 1^{+}$, nærmer nevneren $x-1$ seg $0$ fra oversiden, slik at $f\left(x\right)$ går mot $+\infty$. Dermed får vi en vertikal asymptote i $x=1$.

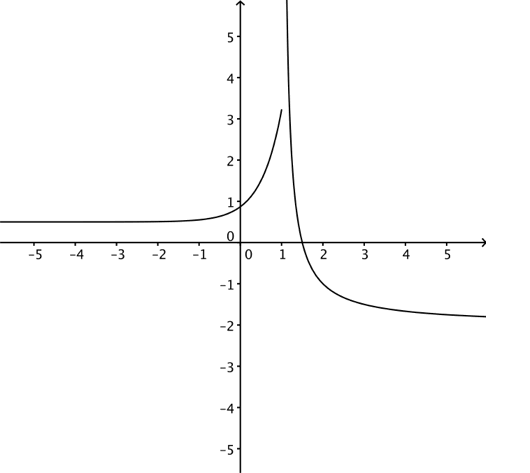
Vi har funnet to horisontale og en vertikal asymptote. Prøv å tegne grafen slik som under og tegne inn asymptotene.