Grenseverdier

Vi begynner med et eksempel. La $f$ være funksjonen gitt ved

 $f\left(x\right)=\frac{x^2-1}{x-1}$.

Vi ser at $f$ ikke er definert for $x=1$, fordi nevneren blir null – man kan ikke regne ut noen verdi da. Men vi kan likevel undersøke hva som skjer med $f\left(x\right)$ når $x$ nærmer seg 1. Av verdiene

 $f\left(0,9\right)=1,9 f\left(0,99\right)=1,99 f\left(0,999\right)=1,999$

 $f\left(1,1\right)=2,1 f\left(1,01\right)=2,01 f\left(1,001\right)=2,001$

er det tydelig at $f\left(x\right)$ nærmer seg 2 når $x$ nærmer seg 1.

Vi kan se dette enda tydeligere ved å foreta et lite forkortingstriks. For alle $x$ bortsett fra $x=1$, har vi nemlig at (husk

Konjugatsetningen

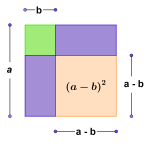
Konjugatsetningen kalles også tredje kvadratsetning:

 $(a+b)(a-b)=a^2-b^2$.

konjugatsetningen

$f\left(x\right)=\frac{x^2-1}{x-1}=\frac{\left(x+1\right)\left(x-1\right)}{x-1}=x+1$.

Fra dette uttrykket ser vi at jo nærmere $x$ kommer 1, desto mer nærmer $f\left(x\right)$ seg 2. I slike situasjoner sier vi at grenseverdien til $f\left(x\right)$ når $x$ går mot 1, er 2. Med symboler skriver vi:

$\underset{x\to 1}{\lim }f\left(x\right)=2$.

Vi formaliserer dette i en definisjon. For å gjøre det lettere å lese, bruker vi notasjonen $x\to a$ for å uttrykke at "$x$ går mot $a$".

En typisk situasjon der grenseverdien ikke eksisterer, er hvis $f\left(x\right)$ vokser mot $\infty$ eller synker mot $-\infty$ når $x\to a$ (for eksempel hvis $f\left(x\right)=\frac{1}{x}$ og $x\to 0$). Selv om grenseverdien i slike tilfeller ikke eksisterer ($\infty$ er ikke noe bestemt tall!), er det likevel vanlig å skrive $\underset{x\to a}{\lim }f\left(x\right)=\pm \infty$.