Union og snitt av mengder
Mengdeoperasjoner fra MatRIC
Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC
DEFINISJON UNION OG SNITT AV MENGDER
La A og B være mengder.
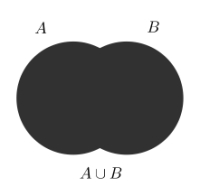
Mengden av alle elementer som er enten i A eller i B (eller i begge), kaller vi unionen av A og B. Vi skriver dette som .Unionen av mengdene A og B
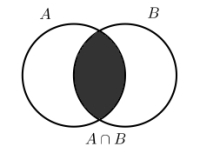
Mengden av alle elementer som er både i A og B, kaller vi snittet av A og B. Vi skriver dette som . Snittet av mengdene A og B
Eksempel 1
La og . Da er og .
Eksempel 2:
I en klasse driver alle elevene med enten fotball eller spiller et instrument, eller begge deler. La være mengden av alle elevene som driver med fotball, og være alle som spiller et instrument. Da er
= hele klassen fordi alle driver med enten fotball eller spiller et instrument.
= alle som både spiller et instrument og spiller fotball.
Eksempel 3
La være mengden av alle partall, altså og være mengden av alle tall som kan deles på 3, altså .
Unionen er da alle tall som kan deles på 3 eller 2.
Snittet blir da alle tall som kan deles på både 3 og 2. Dette er faktisk alle tall som kan deles på 6! Hvorfor? Jo, hvis et tall skal være delbart med både 2 og 3 må det kunne skrives som både og for heltall og . Fra dette kan vi slutte at det også må kunne skrives som for et heltall . (Du kan lese mer om primtallsfaktorisering i artikkelen "Primtall og faktorisering" til høyre.)
Del på Facebook