Direkte bevis

Eksempel 1

Vis at hvis $a$ og $b$ er partall, så er $a+b$ også partall.

Bevis:

Et partall er et tall som kan deles på 2. La $k=\frac{a}{2}$ og $r=\frac{b}{2}$.

Da er $\frac{a+b}{2}=\frac{a}{2}+\frac{b}{2}=k+r$ og dermed er også $a+b$ delelig på 2, så det er et partall.

Eksempel 2

Vis at hvis $a$ er et partall og $b$ er et heltall større enn 0, da er $a^b$ også et partall.

Altså, $a$ er et partall og $b>0$ er et heltall  $\Rightarrow$ $a^b$ er et partall.

Bevis:

$a$ er et partall, hvis og bare hvis vi kan skrive det som $2k$ for et heltall $k$. Vi får dermed

$a^b={\left(2k\right)}^b=2^b{k}^b=2\left(2^{b-1}{k}^b\right)$.

siden $b$ er større enn 0, kan vi trekke ut 2 og vi ser dermed at $a^b$ også er et partall. Her har vi vist resultatet direkte fra forutsetningen.

Eksempel 3

Vis at hvis $a$ er et partall og $b$ er et oddetall, så er $a+b$ et oddetall.

Bevis:

Her må vi først bli enige med oss selv om hva det vil si at noe er et oddetall eller partall.

$a$ er et partall hvis det kan deles på to, og da kan vi skrive det som $a=2k$ for et heltall $k$.

$b$ er et oddetall hvis det ikke kan deles på to, og da kan vi skrive det som $b=2r+1$ for et heltall $r$.

Nå kan vi prøve å bevise påstanden over ved å se på $a+b$:

$a+b=2k+2r+1=2\left(k+r\right)+1$

$k+r=t$  er et heltall, og dermed ser vi at $a+b=2t+1$, så det er et oddetall! Dette fullfører beviset.

Eksempel 4

Vis første

Første kvadratsetning

Første kvadratsetning sier at

 ${(a+b)}^2=a^2+2ab+b^2$.

 

kvadratsetning

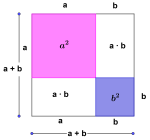
Bevis:

${\left(a+b\right)}^2={\left(a+b\right)\left(a+b\right)=a}^2+ab+ab+b^2=a^2+2ab+b^2$.