Likninger
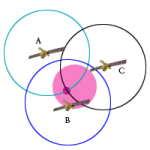
Et av århundrets største oppfinnelser er GPS-systemet. Det kan hjelpe oss til å navigere overalt i verden. Måten GPS fungerer på, er at vi sender ut en signal, og tre (eller flere) satelitter i verdensrommet sender ut deres signaler tilbake. Disse signalene ser ut som sirkler, og der disse tre sirklene møtes, er stedet vi er på. Stedet der de tre sirkelen møtes finner vi ved å bruke likninger. Løsningen til denne likningen er koordinatene til stedet vi er på kartet. Det GPS egentlig gjør, er å løse en gigantisk likning!
En likning kan vi se på som en gammeldags vektskål i balanse. Det er like mye vekt på begge sider, men vektloddene på sidene er i forskjellige størrelser.
Hvis vi legger til et lodd eller tar vekk et lodd på en av sidene, må vi gjøre det samme på den andre siden hvis vekten skal være i balanse. Det samme prinsippet gjelder for likninger. Gjør vi noe på en side av likningen, må vi gjøre akkurat det samme på den andre siden av likningen.
Hvor mye har gått i glemmeboka? Ta en test i
eller
Lynkurs, 8.-10.trinn
Består av:
- Hva er en likning?
- Førstegradslikninger
- Løs en førstegradslikning!
- Andregradslikninger
- Løs en andregradslikning.
- Karoline løser andregradslikninger.
- Likningssystemer
- Grafisk løsning av likningssett
- Prøve- og feilemetoden
- Addisjonsmetoden
- Substitusjonsmetoden
- Inger Christin forteller om likningssystemer.
- Én, mange eller ingen løsninger?
- Inger Christin løser likninger.
- Test deg selv i 1.gradslikninger!
- Test deg selv i likninger!
Begrep
-
Andregradsuttrykk
Et uttrykk på formen , hvor er den størrelsen som varierer, og og er konstante tall.
-
Eksponent
En potens er et tall på formen xn, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.
xn = x · x · x...· x, n ganger -
Ledd
I en addisjon kalles tallene som legges sammen for ledd.
Eksempel: , her kalles tallene 8, 3 og 5 for ledd.
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
Likhetstegn
Likhetsteget har symbolet "".
Likhetstegnet forteller at det som står til venstre for likhetstegnet har samme verdi som det som står til høyre.
Eksempel:
-
Ukjent
I algebra brukes bokstaver for å betegne en ukjent størrelse. En ukjent størrelse kan være et tall som skal tilfredsstille en bestemt ligning.
Eksempel: x + 7 = 16. Her er x en ukjent.