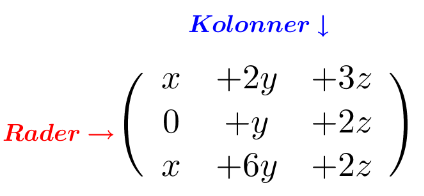Å løse likningssett med matriser

Matriser er et kraftfullt matematisk verktøy for å løse likningssett. La oss se hvordan vi gjør det.

Vi skal illustrere hvordan vi bruker matriser for å løse likninger ved følgende eksempel:

$\begin{matrix} (I) & x + 2 y + 3 z = 6 \\ (II) & y + 2 z = 2 \\ (III) & x + 6 y + 2 z = 5 \end{matrix}$

Matriser

Når vi har tre ukjente (eller flere) kan det fort bli rotete og vanskelig å holde styr på alle likningene. Matriser er et system som gjør det mulig å sette opp likningssett på en ryddig måte. Under får du en kort introduksjon. Du finner mer om matriser i høyrespalten i artikkelen "Kort om matriser og determinanter".

Vi tar utgangspunkt i eksemplet over og setter opp likningssettene som en matriselikning:

$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ x & 6 y & + 2 z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix})$

I en matrise snakker vi om rader og kolonner, slik det er illustrert her:

Legg merke til at vi har organisert likningene slik at hver ukjent har egen kolonne og hver likning har egen rad.

OBS! I denne artikkelen gjør vi en forenkling. Vanligvis vil vi ikke skrive $x, y og z$ i matrisen, vi skriver:

$(\begin{matrix} 1 & 2 & 3 \\ 0 & 1 & 2 \\ 1 & 6 & 2 \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix}) .$

Merke at tallene i matrisen er koeffisientene til $x, y og z$ .

Radoperasjoner

På en matrise kan vi gjøre en rekke operasjoner uten at det endrer løsningen(e) på likningssettet. Disse kaller vi gjerne radoperasjoner.

radoperasjoner i en matrise

1. Legge en rad til en annen rad eller trekke en rad fra en annen.

3. Multiplisere en rad med en konstant.

4. Dividere en rad med en konstant.

5. Bytte plass på to rader.

Eksempel 1

Tidligere har vi lagt sammen likningene på ulike måter når vi har brukt addisjonsmetoden. Nå gjør vi det samme ved å trekke en rad fra en annen eller legge en rad til en annen.

Trykker du på pilen under, vil du se hvordan vi løser likningssettet ved hjelp av addisjonsmetoden. Legg merke til at operasjonene vi gjør ved addisjonsmetoden korresponderer til radoperasjonene vi gjør under.

Løsning av likningssettet ved addisjonsmetoden

Vi eliminerer $x$ ved å trekke likning $(I)$ fra likning $(III)$ :

$\begin{matrix} (III) & x + 6 y + 2 z & = 5 \\ (III) - (I) & x + 6 y + 2 z - (x + 2 y + 3 z) & = 5 - 6 \\ (III *) & 4 y - z & = - 1 \end{matrix}$

Sammen med $(II)$ har vi nå et likningssett med to ukjente:

$\begin{matrix} (II) & y + 2 z = 2 \\ (III*) & 4 y - z = - 1 \end{matrix}$

Vi multipliserer likning $(II)$ med $4$ og trekker fra likning $(III*)$ :

$\begin{matrix} 4 \cdot (II) & 4 y + 8 z & = 8 \\ (III*) & 4 y - z & = - 1 \\ 4 \cdot (II) - (III*) & - 9 z & = - 9 \end{matrix}$

Dette gir oss $z = 1$ . Dette setter vi inn i $(III*)$ , og finner $y = 0$ . Disse løsningene er unike.

Tilslutt setter vi $y = 0 og z = 1$ inn i for eksempel likning $(I)$ :

$\begin{matrix} (I) & x + 2 + 3 z & = 6 \\ x + 2 \cdot 0 + 3 \cdot 1 & = 6 \\ x & = 3 \end{matrix}$

Løsning: $x = 3, y = 0 og z = 1$ .

Vi løser likningssettet ved hjelp av radoperasjoner:

	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ x & + 6 y & + 2 z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 5 \end{matrix})$
$(III) - (I) :$	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ x - x & + 6 y - 2 y & + 2 z - 3 x \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 5 - 6 \end{matrix})$	Trekker rad $(I)$ fra rad $(III)$ ,
	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ 0 & + 4 y & - z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ - 1 \end{matrix})$
$(III) - 4 \cdot (II) :$	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ 0 & + 4 y - 4 y & - z - 4 \cdot 2 z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ - 1 - 4 \cdot 2 \end{matrix})$	trekker 4 $\cdot$ $(II)$ fra rad $(III)$ ,
	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ 0 & 0 & - 9 z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ - 9 \end{matrix})$
$\frac{1}{- 9} \cdot (III) :$	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ 0 & 0 & \frac{- 9 z}{- 9} \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ \frac{- 9}{- 9} \end{matrix})$	dividerer rad $(III)$ på $- 9$ ,
	$(\begin{matrix} x & + 2 y & + 3 z \\ 0 & + y & + 2 z \\ 0 & 0 & z \end{matrix}) = (\begin{matrix} 6 \\ 2 \\ 1 \end{matrix})$

Nå står vi igjen med tre likninger. Rad $(III)$ forteller oss at $z = 1$ . Ved å sette inn for $z$ i rad $(II)$ får vi $y = 0$ . Ved å sette inn for både $z$ og $y$ i rad I finner vi at $x = 3$ . Løsning: $x = 3, y = 0 og z = 1$ .

Eksempel 2

Vi ser på et likningssett med to ukjente:

$\begin{matrix} (I) & x - 2 y = 2 \\ (II) & - x - y = 0 \end{matrix}$

Vi setter det opp som en matrise:

$(\begin{matrix} x & - 2 y \\ - x & - y \end{matrix}) = (\begin{matrix} 2 \\ 0 \end{matrix})$

Nå kan vi bruke radoperasjoner for å løse likningssettet. Vi legger rad $(I)$ til rad $(II)$ for å eliminere $x$ i den andre raden.

$(II) + (I) : (\begin{matrix} x & - 2 y \\ - x + x & - y - 2 y \end{matrix}) = (\begin{matrix} 2 \\ 0 + 2 \end{matrix})$

Vi får

$(\begin{matrix} x & - 2 y \\ 0 & - 3 y \end{matrix}) = (\begin{matrix} 2 \\ 2 \end{matrix})$

Nå kan vi dividere rad $(II)$ med $- 3$ for å få $y$ alene i den nederste raden.

$- \frac{1}{3} (II) : (\begin{matrix} x & - 2 y \\ 0 & - \frac{1}{3} \cdot (- 3 y) \end{matrix}) = (\begin{matrix} 2 \\ - \frac{1}{3} \cdot 2 \end{matrix})$

Fra rad $(II)$ får vi $y = - \frac{2}{3}$ og kan sette inn i rad $(I)$ og få $x = 2 + 2 y = 2 + 2 \cdot (- \frac{2}{3}) = \frac{2}{3}$ .

Løsning: $x = \frac{2}{3} og y = - \frac{2}{3} .$

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Lineære likninger med flere ukjente

Består av:

Tilsvarende emner behandles også i

Kort om matriser og determinanter