Grafisk løsning av likningssett

Noen ganger kan det være lettere å løse et problem ved hjelp av en illustrasjon enn ved en algebraisk utregning. Vi skal se hvordan vi finner løsning til et likningssett ved hjelp av grafer.

Vi skal løse likningssettet:

$\begin{matrix} y - 6 x = 120 & (1) \\ y = 3 x + 150 & (2) \end{matrix}$

Begge likningene (1) og (2) er førstegradslikninger og derfor rette linjer i koordinatsystemet. La oss nå se hvordan vi tegner disse rette linjer.

y skal stå alene på venstresiden.

Vi ønsker å få $y$ alene på venstresiden av likhetstegnet. I likningssettet over er likning (2) på den ønskede formen. For å få $y$ alene på venstresiden i likning (1), legger vi til $6 x$ på begge sider av likningen.

$y - 6 x + 6 x = 120 + 6 x$

$y = 120 + 6 x$

$y = 6 x + 120$

Nå har vi begge likningene i likningssettet på den formen vi ønsker:

$\begin{matrix} y = 6 x + 120 (1) \\ y = 3 x + 150 (2) \end{matrix}$

Regn ut verdier og finn punkter.

Vi velger nå å finne flere ulike verdier for hver av likningene. Vi velger forskjellige verdier for $x$ . Vi setter inn disse i likningen og regner ut tilhørende verdi av $y$ . Dette gir oss tallpar på formen $(x, y)$ . Tallparene er punkter i koordinatsystemet. Strengt tatt trenger vi å finne kun to punkter siden disse bestemmer en linje. Men vi regner ut minst tre slik at vi er sikre på at vi har regnet riktig.

La oss nå regne ut verdier for våre to likninger.

$\begin{matrix} y = 6 x + 120 & (1) \end{matrix}$

Vi velger for $1, 10$ og $20$ som $x$ - verdier og regner ut:

$6 \cdot 1 + 120 = 6 + 120 = 126$

$6 \cdot 10 + 120 = 60 + 120 = 180$

$6 \cdot 20 + 120 = 120 + 120 = 240$

Dette gir oss følgende oppsett:

x	1	10	20
y	126	180	240
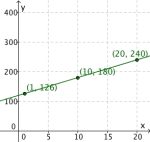
(x,y)	(1,126)	(10,180)	(20,240)

Vi gjør det samme for likning (2). Legg merke til at vi kan bruke de samme verdiene for $x$ som over. Tabellen for likning (2) ser ut som

x	1	10	20
y	153	180	210
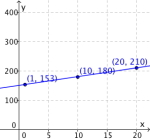
(x,y)	(1,153)	(10,180)	(20,210)

Plott linjene i et koordinatsystem.

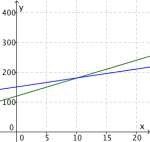
Vi tegner nå punktene $(x, y)$ i et koordinatsystem. Først markerer vi de tre punktene for likning (1) og trekker en rett linje gjennom disse. Dette kalles for grafen til likning (1). Vi gjør det samme med punktene for likning (2). Vi har nå to linjer i koordinatsystemet.


Grafen til (1)	Grafen til (2)	Grafene til (1) og (2)

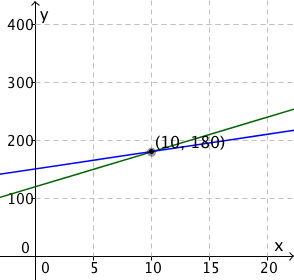
Finn skjæringspunkt.

Skjæringspunktet er løsningen til likningssystemet. Vi ser at linjene skjærer hverandre i punktet $(10, 180)$ , det vil si når $x = 10$ og $y = 180$ . Dette leses av på henholdsvis x-aksen og y-aksen.

Husk at en løsning til et lineært system med to ukjente må ha som svar både en x-verdi og en y-verdi.

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Lineære likninger med flere ukjente

Består av:

Begrep

Akse

Linje eller linjestykke knyttet til symmetri i geometriske figurer, som kalles symmetriakse. Eller en av linjene som spenner ut et koordinatsystem, for eksempel x-akse og y-akse.
Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
Koordinatsystem

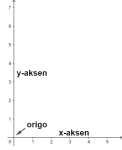
Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).
Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$
Ligningssett

Et ligningssett er to eller flere ligninger med to eller flere ukjente.
Likhetstegn

Likhetsteget har symbolet " $=$ ".

Likhetstegnet forteller at det som står til venstre for likhetstegnet har samme verdi som det som står til høyre.

Eksempel: $6 + 4 = 5 \cdot 2$
Punkt

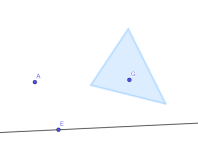
I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.
Skjæringspunkt

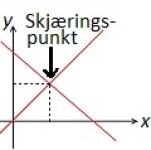
Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.
Tallpar

Beskriver plasseringen av et punkt i et koordinatsystem på formen (x, y).
x-akse

Den horisontale aksen i et koordinatsystem.
Kalles også førsteakse.
y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.