Likningssett med flere enn to ukjente

Likningssett med tre ukjente

Vi løser likningssett med tre ukjente med de samme metodene som vi bruker for å løse likningssett med to ukjente:

1. Bruk substitusjon eller addisjonsmetoden for å komme fram til to likninger med to ukjente. Dette betyr at en av de ukjente må elimineres fra to av likningene.

2. Løs likningssettet med to ukjente ved å bruke substitusjon eller addisjonsmetoden.

3. Sett inn løsningene fra punkt 2. i en av likningene for å finne den siste ukjente.

Eksempel

Vi ser på følgende likningssett med tre ukjente og tre likninger:

$\begin{array}{ccc}\left(\mathrm{I}\right)& & x+2y+3z=6\\ \left(\mathrm{II}\right)& & y+2z=2\\ \left(\mathrm{III}\right)& & x+6y+2z=5\end{array}$

1.

Vi eliminerer $x$ ved å trekke likning $\left(\mathrm{I}\right)$ fra likning $\left(\mathrm{III}\right)$:

$\begin{array}{ccc}\left(\mathrm{III}\right)& x+6y+2z& =5\\ \left(\mathrm{III}\right)-\left(\mathrm{I}\right)& x+6y+2z-\left(x+2y+3z\right)& =5-6\\ \left(\mathrm{III}*\right)& 4y-z& =-1\end{array}$

Sammen med $\left(\mathrm{II}\right)$ har vi nå et likningssett med to ukjente:

$\begin{array}{cc}\left(\mathrm{II}\right)& y+2z=2\\ \left(\mathrm{III*}\right)& 4y-z=-1\end{array}$

2.

Vi multipliserer likning $\left(\mathrm{II}\right)$ med $4$ og trekker fra likning $\left(\mathrm{III*}\right)$:

$\begin{array}{ccc}4\cdot \left(\mathrm{II}\right)& 4y+8z& =8\\ \left(\mathrm{III*}\right)& 4y-z& =-1\\ 4\cdot \left(\mathrm{II}\right)-\left(\mathrm{III*}\right)& -9z& =-9\end{array}$

Dette gir oss $z=1$. Setter vi inn $z=1$ i $\left(\mathrm{III*}\right)$, finner vi $y=0$. Disse løsningene er unike.

3.

Til slutt setter vi $y=0 \mathrm{og} z=1$ inn i for eksempel likning $\left(\mathrm{I}\right)$:

$\begin{array}{ccc}\left(\mathrm{I}\right)& x+2+3z& =6\\ & x+2\cdot 0+3\cdot 1& =6\\ & x& =3\end{array}$

Løsning: $x=3, y=0 \mathrm{og} z=1$. Vi kunne også like gjerne ha brukt substitusjonsmetoden.

Ingen, én eller mange løsninger?

På samme måte som med likningssett med to ukjente, kan vi få ingen, én eller mange løsninger på et likningssett.

Ingen løsning: Hvis det å tilfredsstille én eller to av likningene fører til at den siste blir en motsetning, har vi ingen løsning. Eksempel:

$\begin{array}{ccc}\left(\mathrm{I}\right)& & x+2z=2\\ \left(\mathrm{II}\right)& & y+z=2\\ \left(\mathrm{III}\right)& & x+2z=1\end{array}$

Her ser vi at likning $\left(\mathrm{I}\right)$ og $\left(\mathrm{III}\right)$ ikke kan være sanne samtidig ($x+2z$ kan ikke både være 1 og 2 samtidig) og vi har derfor ingen løsning på likningssettet.

Mange løsninger: Hvis en av likningene er en lineær kombinasjon av de to andre og det finnes løsninger, har likningssettet uendelig mange løsninger. En lineær kombinasjon av to likninger får vi ved å legge sammen en konstant multiplisert med den ene likningen med en konstant multiplisert med den andre likningen. Eksempel:

$\begin{array}{ccc}\left(\mathrm{I}\right)& & x+z=3\\ \left(\mathrm{II}\right)& & y=-1\\ \left(\mathrm{III}\right)& & 2x+y+2z=5\end{array}$

Legg merke til at likning $\left(\mathrm{III}\right)$ er likning $\left(\mathrm{I}\right)$ multiplisert med to pluss likning $\left(\mathrm{II}\right)$: $2\left(x+z\right)+y=2\cdot 3-1$. Dermed får vi at løsningen er $y=-1$ og alle $x$ og $z$ som tilfredsstiller $x=3-z$. Legg merke til at $x=3-z$ definerer en linje og det er uendelig mange løsninger.

Én unik løsning: Én unik løsning får vi hvis vi ikke har noen av tilfellene over. Likningssettet øverst er et eksempel på det!

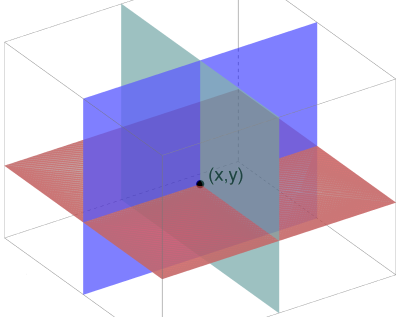
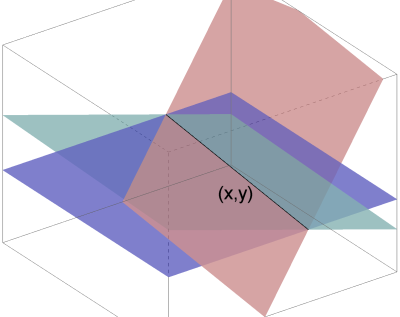
Geometrisk tolkning

Geometrisk kan vi tenke oss et likningssett med 3 ukjente på følgende måte: Hver likning definerer et plan. Løsningen(e) finner vi der alle planene skjærer hverandre. Dette kan være aldri (ingen løsning), i en linje siden to plan skjærer hverandre i en linje (uendelig mange løsninger), eller i et punkt (én løsning).

Én løsning

Ingen løsning

Mange løsninger:

Likninger med flere enn 3 ukjente

Vi kan også løse likninger med flere enn tre ukjente. Vi gjør dette på akkurat samme måte som for tre: vi eliminerer én og én ukjent fra likningssettet til vi ender opp med løsningen for én ukjent. Så bruker vi de andre likningene for å finne de andre ukjente. Se gjerne på artikkelen "Å løse likningssett med matriser", da matriser brukes for å løse likningssett med mange likninger og ukjente.