Grafisk løsning av likninger

La oss starte med en

Vi tegner grafen til venstresiden $f\left(x\right)=-2x+2$ og høyresiden $g\left(x\right)=\frac{1}{2}x-1$. Nå leser vi av $x$-verdien til punktet hvor grafene skjærer hverandre. $x$-verdien er løsningen av likningen.

Vi leser av skjæringspunktet og finner $x=1,2$. Denne verdien av den ukjente gir høyresiden lik venstresiden i likningen. Vi har funnet løsningen av likningen. 

NB: Husk at denne metoden gir en tilnærmet løsning på likningen. Hvis løsningen for eksempel er et

Metoden kan brukes for alle typer likninger.

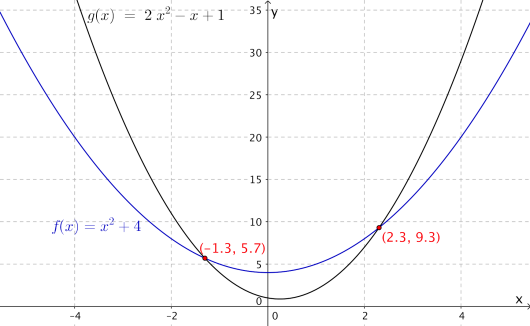
Eksempel 1

Vi har likningen

$x^2+4=2x^2-x+1$.

For å løse denne grafisk setter vi $f\left(x\right)=x^2+4$ og $g\left(x\right)=2x^2-x+1$. Vi tegner grafene og finner skjæringspunktene.

Vi ser at det er to skjæringspunkter (andregradslikninger har to løsninger), nemlig $x=-1,3$ og $x=2,3$.

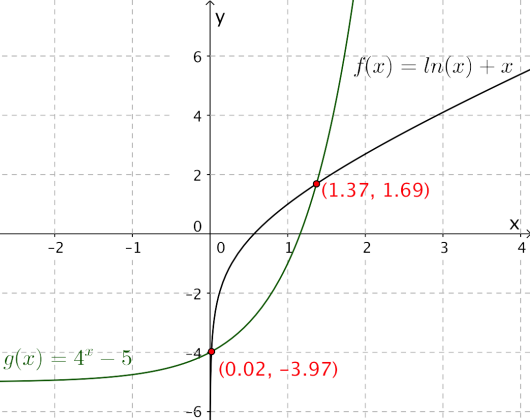
Eksempel 2

Løs likningen $\log \left(x\right)+x=4^x-5$.

Vi lar $f\left(x\right)=\log \left(x\right)+x$ og $g\left(x\right)=4^x-5$. Vi tegner grafene til disse funksjonene og finner skjæringspunktene.

Vi leser av at likningen har to løsninger: $x=0,02$ og $x=1,37$.

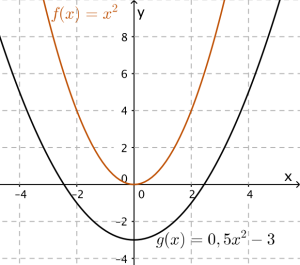
Eksempel 3

Løs likningen $x^2=0,5x^2-3$.

Vi tegner grafene:

Vi ser at grafene ikke skjærer hverandre. Dette betyr at det ikke finnes noen reel løsning. (Det finnes imidlertid en kompleks løsning, men det ligger utenfor dette kursets ramme.)