En kule
Hvordan vi kommer frem til formlene for å beregne overflateareal og volum av ei kule, krever mer avansert matematikk enn vi har mulighet til å gå inn på her. Derfor skal vi begynne med å se på ei halvkule.
Vi tenker oss at ei halvkule ligger oppå en sirkel med samme radius og dekker helt nøyaktig hele sirkelen. Halvkula har et overflateareal som er en god del større enn arealet til sirkelen. Halvkula har faktisk akkurat dobbelt så stor overflate som arealet til sirkelen med samme radius. Det betyr at arealet på ei halvkule med radius er lik . Og overflaten til hele kula er selvsagt to ganger dette. Vi slår derfor fast:
Ei kule med radius har et overflateareal
Hva er kulas volum? La oss tenke oss at kula er satt sammen av mange syltynne pyramider, alle med spissen i kulas sentrum og høyden lik radius i kula.
Den samlede grunnflaten i alle pyramidene er lik kulas overflate . Og disse pyramidene har alle samme høyde som kulas radius . Det betyr at kulas volum er
Husk at pyramidens volum er grunnflaten multiplisert med høyden dividert på tre, , hvor er grunnflaten. Dermed er volumet av kula lik overflaten av kula multiplisert med radiusen dividert på tre.
Vi kan oppsummere. Ei kule med radius har
- overflateareal lik .
- volum lik .
Hvordan vi utleder formelen for volum av kuler og kjegler, lærer du senere. Men hvis du vil ta en titt, se i høyrespalten der Halvar viser deg akkurat dette.
Eksempel
På en fabrikk skal de opprette et lager for flytende ammoniakk. Dette skal lagres på store, kuleformede ståltanker, og hver av tankene bør romme minst . Spørsmål vi kan stille er mange:
- Hvor stor radius og diameter må disse tankene ha?
- Hvor mange kvadratmeter stålplater som går med på å lage tankene?
- Hvor mye vil tomme tanker veie?
- Hvor mye veier tankene når de er fulle?
- Hvordan må dimensjonene være for at de skal tåle trykket av ammoniakken?
Vi begynner med å se på de ytre dimensjonene:
Av formelen for volumet av ei kule kan vi bestemme radius meter for en tank:
gir
Vi regner ut og finner at og dermed kan vi sette . Videre finner vi at , radiusen, blir .
Bedriftsledelsen bestemmer seg for å bygge ståltanker med radius meter. Diameteren er da . En slik ståltank får et volum på
Hvor mange kvadratmeter stålplater trengs? Det må legges et påslagg på for svinn ved tilkapping:
Vi ser at tankenes overflateareal blir
Når vi tar hensyn til svinnet, ser vi at det trengs plater.
Legg merke til at dersom svinn utgjør , ville vi måttet dividere overflatearealet med . Husk alltid å være nøye med hva prosentgrunnlaget er.
Del på Facebook
Lynkurs, 8.-10.trinn
Geometri - areal og volum
Består av:
- Tom forteller om areal
- Et kvadrat
- Et rektangel
- En trekant
- Et parallellogram
- Et trapes
- Tom forteller om overflatearealer
- Overflatearealet til en terning
- Tom forteller om volum
- Et rett prisme
- En sylinder
- Pyramider og kjegler
- En kule
- Pytagoras læresetning
- Tom forteller om formlikhet og Pytagoras læresetning
- Test deg selv i geometri (areal og volum)!
- Test deg selv i tallet π (PI)
Tilsvarende emner behandles også i
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Arealenheter
Mål for areal:
km², m², dm², cm², mm²Andre mål:
1 ar = 100 m2
1 dekar = 10 ar = 1000 m2 = 1 mål
(deka betyr 10)Omgjøring mellom enheter:
1 m² = 1 m · 1 m = 10 dm · 10 dm = 100 dm²
1 dm² = 1 dm · 1 dm = 10 cm · 10 cm = 100 cm²
1 cm² = 1 cm · 1 cm = 10 mm · 10 mm = 100 mm² -
Kule
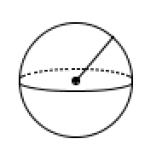
Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.
-
Lengde
Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
-
Volum
Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).