Et trapes

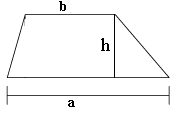
Et trapes er en firkant som har (minst) to parallelle sider, men de kan være av forskjellig lengde.

La oss kalle lengden av de to parallelle sidene for $a$ og $b$ , og sette avstanden mellom dem lik $h$ .

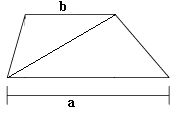
Vi trekker en diagonal slik at vi får to trekanter. Nå kan vi finne arealet til trapeset.

Arealet til hele trapeset er lik summen av arealene til to trekanter. Den nede til høyre har grunnlinje $a$ og høyde $h$ , og arealet av denne blir derfor $\frac{a h}{2}$ . Trekanten oppe til venstre har grunnlinje med lengde $b$ (den sidelengden som er øverst i trapeset), og denne trekanten har også høyde $h$ , og dermed areal $\frac{b h}{2}$ .
Vi legger sammen arealene til trekantene og får at arealet til trapeset er lik

$A = \frac{a h}{2} + \frac{b h}{2}$

Ved å sette på felles brøkstrek og faktorisere telleren, skriver vi formelen på denne måten

$A = \frac{a h + b h}{2} = \frac{(a + b) h}{2}$

Vi har dermed en formel som kan brukes til å beregne arealet av ethvert trapes hvor vi kjenner sidelengdene $a$ og $b$ til de to parallelle sidene og avstanden $h$ mellom disse.

Eksempel

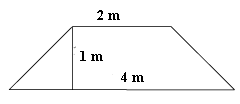
Regn ut arealet av trapeset.

Vi beregner arealet direkte fra formelen:

$A = \frac{(a + b) h}{2} = \frac{(4 + 2) \cdot 1}{2} m^{2} = \frac{6}{2} m^{2} = 3 m^{2}$

Vi kan altså sette verdiene rett inn i formelen og finne at arealet er lik 3 kvadratmeter.

Del på Facebook

Del på Facebook

Lynkurs, 8.-10.trinn

Geometri - areal og volum

Består av:

Begrep

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².
Diagonal

Linjestykke som forbinder to ikke nærliggende hjørner i en mangekant.
Faktorisering

Å faktorisere et tall betyr å skrive tallet som et produkt av to eller flere tall.

Eksempel: 36 = 2 · 18, 36 = 6 · 6, 36 = 2 · 2 · 3 · 3

Se også primtallsfaktorisering
Grunnlinje

Grunnlinja er en av sidene i en todimensjonal figur.

Alle sidene kan være grunnlinje. Når vi skal finne høyden i en trekant, må vi vurdere hvilken av sidene som er mest egnet som grunnlinje.
Høyde

Lengden av et linjestykke som står normalt på ei linje eller en flate.
Lengde

Lengde er målet for avstand. Lengden måles langs linjer, både rette og buede. Enheten for lengde er meter, eller andre mål avledet fra meter.
Parallell

To rette linjer i et plan er parallelle når de ikke skjærer hverandre. Avstanden mellom linjene er den samme uansett hvor du måler.

Tegnet som forteller at to linjer er parallelle: $∥$

Eksempel: $g ∥ f$ , leses "linja g er parallell med linja f".
Teller

Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.

Eksempel: I brøken $\frac{5}{9}$ , er det 5 som er telleren. 9 kalles nevner.
Trapes

Firkant der to sider er parallelle.

Areal = $\frac{(a + b) h}{2}$
Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

Et trapes

Eksempel

Lynkurs, 8.-10.trinn

Geometri - areal og volum

Består av:

Begrep

Areal

Diagonal

Faktorisering

Grunnlinje

Høyde

Lengde

Parallell

Teller

Trapes

Trekant