Hopp til hovedinnholdet
www.matematikk.org

Pyramider og kjegler

Hva er volumet til en pyramide eller en kjegle?

Volum til et prisme finner vi ved å multiplisere høyden, lengden og bredden.
Men verken en pyramide eller en kjegle har samme bredde eller lengde fra grunnflaten og opp til toppen. Pyramider kan ha ulike former av grunnflater; trekant, kvadrat, femkant eller andre. Derfor er volumet til en pyramide lik en tredjedel av grunnflatens areal multiplisert med pyramidens høyde:

Volum av pyramider og kjegler

V=G⋅h3

Hvordan vi utleder formlene for kuler og kjegler, lærer man først på videregående skole. Hvis du har lyst å se hvordan det gjøres, se i høyrespalten der Halvar viser akkurat dette.

En

Kjegle

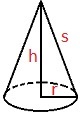
Kjegle

En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.

Kjeksen til en kroneis har form som en kjegle.

Volum : V = π⁢r2h3
Overflate : A = πr2⁢+ πrs 

kjegle
med en sirkel med radius r som grunnflate og høyde h har volum lik

 V=13πr2h 

 

Volum til en pyramide eller kjegle er altså lik en tredjedel av hva det hadde vært for en eske eller sylinder med samme grunnflate.

 

Eksempel

Den store pyramiden i Giza i Egypt er verdens mest kjente pyramide. Pyramiden er 138,8 meter høy og den har en kvadratisk grunnflate med 230,4 meter per side. Vi antar at pyramiden er hul inni. Hvor mye vann trengs det for å fylle hele pyramiden?

Vi må først finne ut av hva grunnflaten er, altså hva arealet av pyramidens kvadratiske bunn er.

 G=(230,4 m)2=53084,16 m2 

Pyramiden har et kjempe areal! Vi kan nå sette inn høyden og grunnflaten inn i formelen.

 V=53084,16 m2⋅138,8 m3=2456027,136 m3≈2456027 m3 

Dette er et enormt tall! 2456027 m3 utgjør  2 456 027 000 liter!

Del på Facebook

Del på Facebook

Lynkurs, 8.-10.trinn

Geometri - areal og volum

Består av:

Tilsvarende emner behandles også i

Begrep

  • Areal

    Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
    Noen måleenheter for areal er m2, dm2 og cm2.

  • Arealenheter

    Mål for areal:
    km², m², dm², cm², mm²

    Andre mål:
    1 ar = 100 m2
    1 dekar = 10 ar = 1000 m2 = 1 mål
    (deka betyr 10)

    Omgjøring mellom enheter:
    1 m² = 1 m · 1 m = 10 dm · 10 dm = 100 dm²
    1 dm² = 1 dm · 1 dm = 10 cm · 10 cm = 100 cm²
    1 cm² = 1 cm · 1 cm = 10 mm · 10 mm = 100 mm²

  • Kjegle

    Kjegle

    En kjegle er en tredimensjonal figur som består av en grunnflate som samles i et punkt over flaten.

    Kjeksen til en kroneis har form som en kjegle.

    Volum : V = π⁢r2h3
    Overflate : A = πr2⁢+ πrs 

  • Lengdeenhet

    Måleenheten for lengde er meter med forkortelsen m. Andre lengdemål avledet av meter er: kilometer (km), desimeter (dm), centimeter (cm) og millimeter (mm).

  • Meter

    Meter er måleenheten for lengde og forkortes m. Mange andre lengdemål er avledet av meter:

    kilometer: 1 km = 1000 m
    desimeter: 10 dm = 1 m
    centimeter: 100 cm = 1 m
    millimeter: 1000 mm = 1 m

  • Pyramide

    Pyramide

    Et objekt som består av en mangekantet grunnflate, med sideflater som er trekantede. Trekantene møtes i en spiss som utgjør et hjørne av pyramiden.

     

  • Volum

    Volum

    Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm3) og kubikkmeter (m3).

Hopp over bunnteksten