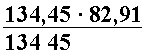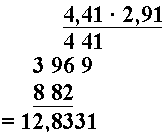Multiplikasjon av desimaltall

Multiplikasjon av desimaltall ved hjelp av areal

Eksempel

Regn ut

$3,2\cdot 2,3$

• Hvor mange hele får vi?
• Hvor mange tideler får vi ?
• Hvor mange hundredeler får vi?

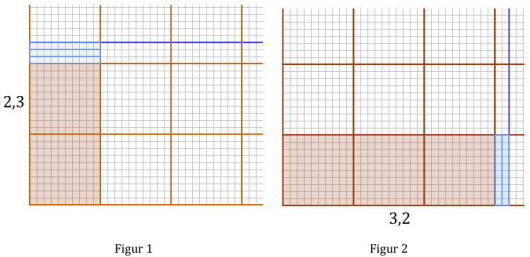
Vi kan dele inn et ruteark. Vi markerer $2,3$ som vist på figur 1, og $3,2$ som vist på figur 2.

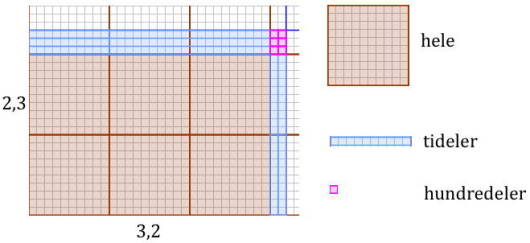
Multiplikasjon betyr at vi kan fargelegge følgende areal

Vi ser av illustrasjonen at vi har seks hele (brune kvadrater bestående av 10 x 10 små kvadrater), $13$ tideler (blå rektangler bestående av $1\times 10$ små kvadrater der ni er vannrette og fire loddrette), og seks hundredeler (rosa kvadrater). Siden $13$ tideler består av en hel og tre tideler, blir derfor svaret

$7$ hele, $3$ tideler og $6$ hundredeler, altså

$3,2\cdot 2,3=7,36$

Multiplikasjon av desimaltall ved oppstilling

Eksempel

Regn ut $134,45\cdot 82,91$.

Her vil nok de aller fleste måtte melde pass i forhold til å regne i hodet. Vi må bruke en skriftlig oppstilling. La oss gjøre et overslag først, slik at vi kan ha en mening om størrelsen på svaret:

$134,45\cdot 82,91\approx 140\cdot 80\approx 11000$

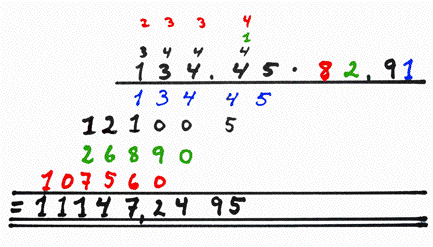
I likhet med multiplikasjonen med hele tall multipliserer vi ett og ett siffer fra faktoren til høyre inn i hele faktoren til venstre. Her har vi multiplisert inn tallet 1, men vi lar foreløpig være å skrive komma i mellomsvaret.

Det kommer etter at vi har regnet med de øvrige sifrene og skal finne det endelige svaret. Plassen vi setter kommaet på i svaret avhenger av antall desimaler i begge de to faktorene. Antall desimaler i resultatet er faktisk lik summen av antall desimaler i begge faktorene. I vårt tilfelle har begge faktorene to desimaler, så resultatet skal ha fire desimaler.

Vi kan fortsette utregningen slik:

Vi setter delresultatene over hverandre, og passer på å forskyve en plass mot venstre for hver gang vi går til et nytt siffer i faktoren til høyre. Til slutt legger vi tallene sammen, og setter komma slik at vi får fire desimaler.

Har du tenkt over hvorfor vi forskyver mot venstre? Etter første multiplikasjon, er neste siffer ti ganger så stort, så hundre ganger så stort og så videre. Vi kunne altså gjerne ha satt inn en ekstra null til høyre, for hver gang vi bruker et nytt siffer.

En observasjon: Resultatet er i god overensstemmelse med overslaget. 

Multiplikasjon med desimaltall, hvorfor fungerer oppstillingen?

Vi ser på et annet eksempel slik at det er enklere å se sammenhengene. La oss se på  $4,41\cdot 2,91$. Nøkkelen er å dele tallene opp i flere ledd. Vi skal se på hvorfor svaret får fire desimaler, slik som regelen sier oss.

$4,41$ er lik $4$ enere, $4$ tideler og $1$ hundredeler.
$2,91$ er lik $2$ enere, $9$ tideler og $1$ hundredel.

Nå bruker vi fordelingsregelen. Vi multipliserer de tre ensifrede tallene som vi har delt 4,41 opp i, med de tre ensifrede tallene som vi har delt 2,91 opp i. I alt blir det ni multiplikasjoner.

Vi får

$4,41\cdot 2,91=$ 

$4\cdot 2+4\cdot 0,9+4\cdot 0,01+$ 

$0,4\cdot 2+0,4\cdot 0,9+0,4\cdot 0,01+$ 

$0,01\cdot 2+0,01\cdot 0,9+0,01\cdot 0,01$ 

Vi tar for oss en enkelt detalj: $4\cdot 0,9$. Vi vet at 0,9 er tidelen av 9. Da må $4\cdot 0,9$ være tidelen av $4\cdot 9$, altså 3,6. På samme måte gjør vi de andre delutregningene. De to siste desimalene i faktorene ender opp som hundredeler, og hundredeler multiplisert med hverandre gir titusendeler, altså fire desimaler. Her ligger begrunnelsen for antall desimaler i det endelige svaret.

For å få det mer i overensstemmelse med den oppstillingen vi hadde foran, kan vi bytte rekkefølge, slik at stykket blir

$$\begin{gathered} 4,41\cdot 2,91= \\ 0,01\cdot 0,01+0,4\cdot 0,01+4\cdot 0,01+ \\ 0,01\cdot 0,9+0,4\cdot 0,9+4\cdot 0,9+ \\ 0,01\cdot 2+0,4\cdot 2+4\cdot 2 \\ =0,0441+3,969+8,82 \\ =12,8331 \end{gathered}$$

Da kjenner vi igjen alle detaljene i denne oppstillingen:

Hadde vi for eksempel hatt én desimal i den ene faktoren, og fire i den andre, ville vi fått tideler multiplisert med titusendeler, som igjen ville gitt hundretusendeler. Da ville vi endt opp med fem desimaler i svaret.