Sammenhengen mellom røtter og potenser

Vi har hittil bare tatt for oss potenser der eksponentene var hele tall. Vi kan, hvis vi forutsetter at grunntallet $a \geq 0$ , også definere potenser der eksponentene ikke er hele tall, men hvilke som helst positive tall, for eksempel en brøk.

La oss først prøve oss med en potens av a med eksponent $\frac{1}{2}$ . Denne potensen kan vi skrive $a^{\frac{1}{2}}$ . Men hva skal dette bety?

Vi forutsetter at regnereglene for potenser fortsatt skal gjelde. Vi husker for eksempel at:

${(a^{m})}^{n} = a^{m \cdot n}$ .

Vi setter nå inn $m = \frac{1}{2}$ og $n = 2$ , og får

${(a^{\frac{1}{2}})}^{2} = a^{\frac{1}{2} \cdot 2} = a^{1} = a$ .

Men i avsnittet om kvadratrøtter ser vi at ${(\sqrt{a})}^{2} = a$ . Dermed er både ${(a^{\frac{1}{2}})}^{2} = a$ , og ${(\sqrt{a})}^{2} = a$ . Det betyr at vi må definere $a^{\frac{1}{2}} = \sqrt{a}$ . Helt tilsvarende vil vi finne at $a^{\frac{1}{3}} = \sqrt[3]{a}$ , siden

${(a^{\frac{1}{3}})}^{3} = a^{\frac{1}{3} \cdot 3} = a$ .

Vi forstår at $a$ opphøyd i $\frac{1}{n}$ kan settes som $n$ -te rota til et tall $a$ , $a^{\frac{1}{n}} = \sqrt[n]{a} .$

Kan vi ha en potens med brøk der telleren er forskjelling fra 1 som eksponenten? Ja.

Husk at $\frac{m}{n} = m \cdot \frac{1}{n}$ .

Denne regelen sammen med potensregelen gir oss at et grunntall $a$ opphøyd i en brøk $\frac{m}{n}$ er lik

$a^{\frac{m}{n}} = a^{m \cdot \frac{1}{n}} = {(a^{m})}^{\frac{1}{n}} = \sqrt[n]{a^{m}}$ .

Definisjon

For et tall

a \geq 0

og en brøk

\frac{m}{n}

sier vi at

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

Legg merke til at vi like gjerne kunne ha skrevet:

$a^{\frac{m}{n}} = a^{\frac{1}{n} \cdot m} = {(a^{\frac{1}{n}})}^{m} = \sqrt[n]{a^{m}}$ .

Dette forteller oss at $a^{\frac{m}{n}} = \sqrt[n]{a^{m}}$ .

Eller sagt med ord: Vi kan opphøye i en potens og trekke ut rot av et tall i vilkårlig rekkefølge. Resultatet blir likt.

Eksempel 1

Vi vil regne ut $16^{\frac{3}{4}}$ . Det kan vi nå gjøre på forskjellige måter.

$16^{\frac{3}{4}} = \sqrt[4]{16^{3}} = \sqrt[4]{{(2^{4})}^{3}} = \sqrt[4]{2^{3 \cdot 4}} = \sqrt[4]{12^{12}} = 2^{\frac{12}{4}} = 2^{3} = 8$

Alternativt:

$16^{\frac{3}{4}} = {\sqrt[4]{16}}^{3} = {\sqrt[4]{{(2}^{4})}}^{3} = {(2^{\frac{4}{4}})}^{3} = 8$ .

Del på Facebook

Del på Facebook

Lynkurs 11.-13.trinn

Potenser og røtter

Består av:

Begrep

Brøk

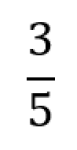
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.
Eksponent

En potens er et tall på formen xⁿ, der verdien til n forteller hvor mange ganger vi ønsker å multiplisere x med seg selv. n kalles eksponenten.

xⁿ = x · x · x...· x, n ganger
Grunntall

En potens består av et grunntall og en eksponent.

Eksempel: 4 · 4 · 4 kan skrives som 4³ , der 4 er grunntall og 3 er eksponent.
Heltall

Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3...

Symbolet for mengden av hele tall er ℤ.
Kvadratrot

Kvadratrot har symbolet $\sqrt{}$ .

Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.

Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi $4 \cdot 4 = 16$ . Det skrives $\sqrt{16} = 4$ .
Positive tall

Tall som er større enn null kalles positive tall.

Eksempel: 1, 78, 435.
Potens

En potens består av et grunntall opphøyd i en eksponent. Eksponenten sier hvor mange ganger grunntallet skal multipliseres med seg selv. En potens skrives på formen $x^{n}$ , som leses x opphøyd i n-te.

Eksempel: $4^{3} = 4 \cdot 4 \cdot 4$
Rot

Se Kvadratrot

Sammenhengen mellom røtter og potenser

Eksempel 1

Lynkurs 11.-13.trinn

Potenser og røtter

Består av:

Begrep

Brøk

Eksponent

Grunntall

Heltall

Kvadratrot

Positive tall

Potens

Rot