Andre kvadratsetning
Nå skal vi se på en regel som hjelper oss å forkorte brøker, forenkle utrykk og løse likninger.
Den andre kvadratsetningen er et uttrykk for produktet av differansen mellom to tall.
La oss se regne ut . Husk at og .
Utregningen gir oss at
Akkurat dette kalles andre kvadratsetning!
Den andre kvadratsetningen
Eksempel
La oss se at dette stemmer når og er tall.
La og . Vi setter inn for og i , og får:
Vi setter inn for a og b i , og ser at resultatet blir det samme:
Andre kvadratsetning
Rettighetshaver: UiO /
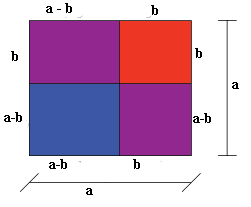
Geometrisk illustrasjon og begrunnelse
Nå skal vi finne arealet til det blå kvadratet på to ulike måter. Først kan vi se på arealet som produktet av høyden og lengden som i et kvadrat er like lange. Det blå kvadratet har sidelengder . Arealet til kvadratet er .
Den andre måten å finne arealet av det blå kvadratet er å først finne arealet til hele det store kvadratet og så trekke fra arealene til lilla rektangler og det røde kvadratet. Arealet av det store kvadratet er lik . Hvert lilla rektangel har areal lik . Det røde kvadratet har areal lik . Da er arealet til det blå kvadratet lik
.
Nå ser vi at vi har funnet arealet av det samme kvadratet på to ulike måter, men det er fortsatt akkurat det samme arealet. Derfor må de to uttrykkene være like,
Det er jo akkurat den andre kvadratsetningen!
Del på Facebook
Lynkurs, 8.-10.trinn
Algebra
Består av:
- Hvorfor regne med bokstaver?
- Regnereglene
- Parenteser og faktorisering
- Regning med fortegn
- Inger Christin forteller om regning med fortegn.
- Fortegn foran parenteser
- Første kvadratsetning
- Andre kvadratsetning
- Konjugatsetningen
- Hvordan bruke kvadratsetningene?
- Løsning av førstegradslikning
- Løsning av andregradslikning
- abc-formelen
- Inger Christin regner med brøker og bokstaver.
- Å fullføre kvadratet
- Test deg selv i bokstavregning I!
- Test deg selv i bokstavregning II!
- Test deg selv i kvadratsetningene!
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.