Første kvadratsetning
Her skal vi se på en regel som hjelper oss å forkorte brøker, forenkle utrykk, og å løse likninger.
Første kvadratsetning beskriver hvordan vi kan skrive summen av to tall multiplisert med seg selv.
La oss regnet ut .
Uten mellomregningen har vi at
Dette kalles den første kvadratsetningen.
den første kvadratsetningen
Eksempel
I eksempelet nå viser vi at likheten stemmer når vi bruker tall i stedet for og .
La og . Da er
Vi får samme resultat akkurat slik første kvadratsetningen sier vi skal!
Første kvadratsetning
Rettighetshaver: UiO /
Geometrisk illustrasjon og begrunnelse
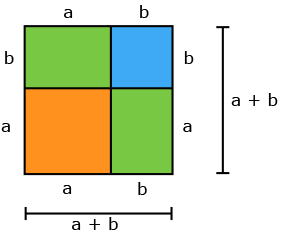
En grunn til å kalle dette første kvadratsetning er at for positive tall og , tolkes som arealet av et kvadrat med sidelengde . Arealet til dette kvadratet kan vi finne på to måter. Først kan vi si at arealet av kvadratet er produktet av lengden og høyden,
.
Men vi kan også få arealet av kvadratet ved å legge sammen arealene til det oransje kvadratet, det blå kvadratet og de to grønne rektanglene.
- Areal av oransje kvadrat: .
- Areal av blå kvadrat: .
- Areal av grønt rektangel: .
Legger vi sammen de fire arealene får vi
.
Begge uttrykkene,
og
,
står for det samme arealet og derfor er . Men dette er jo første kvadratsetning!
Del på Facebook
Lynkurs, 8.-10.trinn
Algebra
Består av:
- Hvorfor regne med bokstaver?
- Regnereglene
- Parenteser og faktorisering
- Regning med fortegn
- Inger Christin forteller om regning med fortegn.
- Fortegn foran parenteser
- Første kvadratsetning
- Andre kvadratsetning
- Konjugatsetningen
- Hvordan bruke kvadratsetningene?
- Løsning av førstegradslikning
- Løsning av andregradslikning
- abc-formelen
- Inger Christin regner med brøker og bokstaver.
- Å fullføre kvadratet
- Test deg selv i bokstavregning I!
- Test deg selv i bokstavregning II!
- Test deg selv i kvadratsetningene!
Begrep
-
Areal
Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m2, dm2 og cm2. -
Rektangel
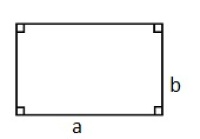
Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.
Areal:Omkrets: